Biomechanical Response in Mandibular Bone due to Mastication Loading on 3-Unit Fixed Partial Dentures
- Clarice Field c.field{at}usyd.edu.au1
- Qing Li q.li{at}usyd.edu.au1
- Wei Li wei{at}aeromech.usyd.edu.au1
- Michael Swain mswain{at}mail.usyd.edu.au2
Abstract
An understanding of functional responses in oral bone is a crucial component of dental biomechanics. The purpose of this study was to investigate the potential biological remodelling response during mastication on the mandibular pre- and post-insertion of a fixed partial denture (FPD). A series of three-dimensional (3D) finite element analysis (FEA) models were presented pre- and postextraction to determine the biomechanical responses to masticatory loading in the anterior mandible. Equivalent strains were analysed at lingual/buccal and mesial/distal areas of the premolar to molar region and quantified to anticipate bone remodelling response. Mandibular bone incorporating an FPD experienced substantially greater stress/strain magnitudes than that prior to placement of fixed prosthodontics, which is suggestive of engagements of bone remodelling. The results suggest similar outcomes to those reported clinically. Developing a simulation reflecting the outcomes of restorative treatment can provide meaningful insight into restorative treatment planning, clinical outcomes, and fixed prosthodontics designs.
1. Introduction
Stress/strain redistributions occurring within mandibular bone as a result of prosthodontic treatments are highly complex and an understanding of the biomechanical factors (strains) initiating bone remodelling due to prosthodontic procedures has not been conclusive so far [1]. For this reason an in-depth understanding of the biological activity in the supporting abutments and bone structures is required as a means for possible improving the outcomes of such restorations. Therefore a detailed biomechanical model becomes essential, especially in typical clinical cases, in order to develop a computational biomechanical simulation capable of identifying the quantitative mechanical response to fixed prosthodontic treatment.
Fixed Partial Dentures are commonly used as a conservative prosthodontic treatment option in restorative dentistry with proven clinical reliability [2, 3] and have played an integral role in the rehabilitation of oral function for years. However, the rigid construction of FPD systems changes the local biomechanical status, whereby bone may model and remodel to accommodate a new loading environment. Thus a critical factor that determines the long-term success of FPDs is how occlusal forces are transferred to the surrounding root abutments, periodontal ligament (PDL), and bone. Bone remodelling is dependent on the maximum load experienced throughout its load history [4]; however, remodelling is also characterised by the number of daily cycles that are consistent with mastication [5, 6]. In typical three-unit fixed partial dentures, the tooth root abutment-bone interface must be able to tolerate changes in occlusal force behaviour without instigating adverse bone tissue responses. In this sense, understanding the effect of biomechanics on biological response is a key step to optimal design of an FPD. In general, the three main biomechanical issues related to an FPD are (1) mechanical loading, (2) transmission of the load to the interfacial tissues, and (3) biological reactions of surrounding tissues to the transmitted load [7].
The quantity and quality of bone depend on its functionality and remodelling responses [8]. There have been a number of phenomenological remodelling theories available for different bone sites [9]. Frost's mechanostat theory is one of such which defines a threshold Minimum Effective Strain (MES) as a mechanical stimulus to trigger bone remodelling [10]. Frost's theory has been applied to various studies [11, 12]. An MES remodelling threshold has been suggested in the range of 0.0008–0.002 unit bone surface strain, below which it is suggestive of bone resorption and above which it is indicative of bone apposition.
Clinically, an FPD can be established immediately upon tooth extraction or more often upon extraction socket healing. Resorption is an inevitable consequence of extraction of a natural tooth due to local bone disuse. Although the resorption may not be eliminated completely, its severity can be reduced by ensuring that the prosthesis transmits mechanical loads to the underlying bone structure properly [13, 14].
Previous investigations [15, 16] conducted on fixed prosthodontics have mainly focused on technical complications and stress peaks within the prosthetic devices. While in other clinical scenarios, tooth-implant systems incorporating an FPD has been evaluated [17–19] for assessing bone-implant osseointegration. Despite their relevance, limited studies have been reported on the biomechanical responses of mandibular bone as a consequence of fixed prosthodontics. Indeed, the complexity of biological reactions surrounding an FPD have made it very difficult to draw general conclusions about the prognosis of restorative treatments with FPDs in general dental practice [20].
This paper aims to establish the stress/strain patterns in mandibular bone to identify the initial status of remodelling stimulus, thereby correlating the finite element (FE) results with clinical observation. In order to achieve a precise quantitative analysis of the initial mechanical responses to loading on an FPD, a biomechanical model is essential as the detailed anatomical configuration of dental structures could largely affect their behaviours [21, 22]. For this reason, computerized-tomograph- (CT-) based 3D finite element analysis (FEA) techniques will be employed in this study to understand the biomechanics in the PDL-bone interface contiguous to abutments of an FPD. It is expected that an increased knowledge in this region can help establish a quantitative relationship associated with biological reactions such as bone remodelling.
2. Material and Methods
This study primarily focuses upon mandibular bone predictive or modelled strain responses as a direct result of mastication. Three-dimensional computational models of a section of the mandible with teeth were established in this study, representing the right mandibular premolar, first and second molars, and their supporting dental apparatus with/without a three-unit fixed partial denture. The finite element models employed in this study were constructed primarily using Computerized Tomography (CT) images, digital edge detection technique, and computer aided design (CAD) methods [23–25].
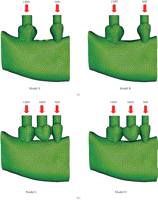
In the present paper, Models A and B are of prefixed prosthodontics initially upon first molar extraction and following a healing period of 12-months without FPD construction, respectively. Models C and D are presented following the three-unit FPD established upon initial tooth extraction and after a 12 month healing period. The extracted tooth model (Models A and C) simulated the removal of the first right molar and the wounded bone structure, immediately after extraction. Bone morphology upon extraction results in the localised extraction sockets which vary between 2.0 and 4.5 mm [26] with a width decrease up to approximately 50% as well as an unchanged the mesial/distal attachment [27]. The healed tooth model (Models B and D) incorporates the first right molar bone socket area of extraction after a 12-month healing period. The fresh bone socket is healed with a pocket depth of 1.1 mm, width of 7.6 mm, and mesial/distal attachment levels of 0.3 mm [27]. This study will compare the mechanical strains within mandibular bone between the extracted and healed scenarios with prefixed prosthodontics and FPD situations.
Models A, B, C, and D (Figure 1) were the basis for the comparative FE analyses that were conducted in ABAQUS 6.6.1 (ABAQUS, Inc, Providence, RI). The models consisted of a 10-node quadratic tetrahedral solid mesh. To establish these four models, relevant convergence tests were performed to determine the best balanced accuracy and efficiency of numerical simulation, as in [24], which led to a global element edge length of 1 mm to ensure the sophistication of the models and an optimal computational cost. Finally, Models A, B, C, and D consisted of 124 196 (DOF: 897 516), 115 675 (DOF: 836 202), 124 520 (DOF: 900 975) and 116 781 (DOF: 847 851) quadratic elements, respectively.
The models were subjected to occlusal forces which functionally varied for each tooth and the FPD. Loads of 50 N, 100 N, and 150 N were applied to the second premolar, first molar, and second molar, respectively (Figure 1). Vaillancourt [28] suggested that an adequate functional loading of 50 N is sufficient for a premolar. Schwarz [29] stated that the molar region can endure mastication forces of up to 3 times greater than the force experienced in the canine region. Thus, mastication forces in this study are classified within an upper range of normal bitting forces [30, 31]. Three-dimensional surface-to-surface contact with solid foods was modelled with a friction coefficient of 0.2 [32], as defined in ABAQUS (Figure 1).
All the materials were presumed linear, elastic, homogeneous, and isotropic for the analyses as widely adopted in existing literature [33, 34] (Table 1). The periodontal ligament (PDL) stress-strain experienced in this paper is well fitted to the linear elastic range for the strains of higher than 5% but less than 20% [35]. Although PDL is viscoelastic in nature, the isotropic elastic properties were assigned as the load response lies within the linear elastic range. Bone in this study is also modelled isotropically like previous studies [26, 36]. Isotropic models of the mandible were able to distinguish meaningful strain differences when replicating functional loading [23], which have been widely accepted by clinicians when evaluating patients [37].
Material properties required within the FEA models [25].
The FE analyses of Models A, B, C, and D primarily focused upon the stresses and
strains within the alveolar and cortical bony tissues. The biomechanical differences
due to mastication in the pre-FPD and FPD cases are evident within the contiguous
bone. Numerical values for strains in the extracted and healed cases were taken from
distal, mesial, lingual, and buccal sites. Each site contained five representative
reading points. Comparisons between the models were made through the von Mises
stresses, principal stresses, and equivalent strains. Firstly, von Mises stresses
were evaluated to provide distortion energies as an indicator to overall tissue
deformation. Then, the first and third principal stresses were characterised to
highlight tension and compression behaviours in these specific sites, where the
nature of these stresses may affect bone remodelling. Finally, the equivalent
strains were acquired to enable a measure of quantifying instigators into bone
remodelling. Equivalent strain represents an aggregate elastic distortion within the
bony tissues, which can be calculated from components of principal strains
(e1, e2,
e3) as follows [38]: 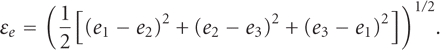
According to Frost's remodelling theory [39], the equivalent strain is considered one of the most appropriate indicators of effectively predicting bone remodelling.
3. Results
The finite element analyses indicated that the elevated von Mises stresses occurred in the cortical ridges of functionally loaded teeth, suggesting high distortion energy distributions there. The maximum von Mises stresses are located around the second molar roots at the lingual site in Model A and the distal region in Models B, C, and D. Their corresponding values are 37.5 MPa, 36.2 MPa, 27.3 MPa, and 23.3 MPa, respectively.
The maximum first principal stresses in mandibular bone of Models A and B (without FPD) were situated at the cortical ridge about the mesial aspect of the second molar, which were 10.2 MPa and 11.5 MPa, respectively. It is noted that the freshly extracted case has a slightly lower tensile stress peak than the healed case. The maximum first principal stresses in Models C and D (with FPD) were located about the distal region of the second molar and were 25.1 MPa and 21.9 MPa, respectively, in which the FPD in the healed case presents a 15% lower tensile stress peak. It is noted that all these first principal stress peaks are positive, indicating a tension in the surrounding areas.
The maximum third principal stresses in the mandibular bone were situated in the lingual region of the cortical ridge in Models A, B, C, and D, where the peak values were −58.1 MPa, −57.7 MPa, −16.9 MPa, and −15.5 MPa, respectively. It is noted that all these third principal stress peaks are consistently negative, indicating a compressive nature at these sites. A comparison of the first and third principal stress peaks about the first molar are summarised in Table 2.
Principal stress distributions within mandibular bone about the first molar.
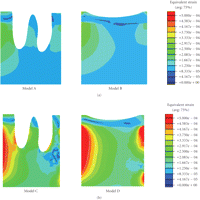
As shown in Figure 2, the peak
equivalent strains on the ridged regions of the cortical bone were located in the
lingual area in Models A and B (without FPD), showing 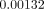 and
and 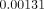 ,
respectively. In Models C and D (with FPD), the maximum equivalent strains were
situated around the root apex of the second premolar, yielding
,
respectively. In Models C and D (with FPD), the maximum equivalent strains were
situated around the root apex of the second premolar, yielding
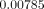 and
and 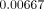 ,
respectively. The minimum equivalent strains Models A, B, C, and D are
,
respectively. The minimum equivalent strains Models A, B, C, and D are
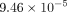 ,
,
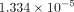 ,
,
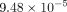 ,
and
,
and 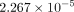 .
It is noted that the equivalent strain in the ridged regions of the cortical bone is
of primary interest in determining initiation of bone remodelling. The corresponding
average values for the equivalent strain in the mesial sides around the first molar
region in Models A, B, C, and D were 0.0002∊,
0.0006∊, 0.0005∊, and
0.0012∊, respectively, while they were
0.0006∊, 0.0008∊,
0.0013∊, and 0.002∊ on the
distal sides, respectively.
.
It is noted that the equivalent strain in the ridged regions of the cortical bone is
of primary interest in determining initiation of bone remodelling. The corresponding
average values for the equivalent strain in the mesial sides around the first molar
region in Models A, B, C, and D were 0.0002∊,
0.0006∊, 0.0005∊, and
0.0012∊, respectively, while they were
0.0006∊, 0.0008∊,
0.0013∊, and 0.002∊ on the
distal sides, respectively.
Tooth extraction significantly altered the equivalent strain concentrations around the first molar (Figure 3). The average lingual strains in Models A, B, C, and D were 0.0002∊, 0.0005∊, 0.0002∊, and 0.0004∊, while the average buccal strains were 0.0001∊, 0.0002∊, 0.0002∊, and 0.001∊, respectively.
4. Discussion
In order to gain understanding of the consequences of FPD treatment, it is essential to establish a sound knowledge of the physiological characteristics of all the supporting tissues within such an oral environment. A fundamental design criterion for an FPD is to institute compatibility with its surrounding living tissues. The vitality of bone about an FPD is of primary importance as the condition of bone can in turn affect the stability of the FPD considerably [40]. From the clinician's point of view, it is imperative that the selected abutment teeth for the FPD are supported by adequately healthy alveolar bone [41, 42]. However, it has remained unclear how the alteration of local oral condition induced by extraction of natural tooth and construction of FPD could affect the alveolar bone. Therefore there is a need to quantify the mechanical responses of alveolar bone due to construction of FPD. In this study the stress and strain distributions were examined in the pre-FPD and post-FPD cases within the mandible.
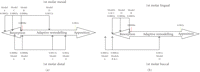
Certain levels of mechanical masticatory stimulation is vital in maintaining sufficient underlying bone health [8]. Tooth extraction leads to immediate changes in local bone morphology and loadings, which consequently alter the biomechanical responses in the surrounding bone bed. Frost's mechanostat theory suggests that the minimum effective strain (MES) in the range of 0.0008–0.002 enables the dynamics of bone turnover to reach equilibrium [10].
In this study, the equivalent strains in the different scenarios yielded the strains within, above, and below Frost's bone adaptive MES remodelling range. The FE analyses showed that the equivalent strains in the cortical ridge of the first molar in the mesial, distal, and buccal regions in Model D (healed with FPD) were within the equilibrium range (Figures 4 and 5). This is a realistic indication that an FPD treatment could better maintain an appropriate bone remodelling equilibrium, thereby preserving a healthy status of bone.
(a) Mesial/distal strains and (b) lingual/buccal strains within in the cortical ridge of the 1st molar in all three cases evaluated with Frost's bone mechanostat (not to scale).
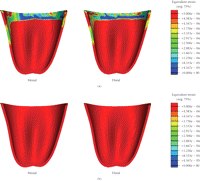
Equivalent strain contours in mandibular bone (a) prebridgework models and (b) FPD models indicating mandibular bone apposition (red), resorption (blue), and equilibrium (green).
It is also seen that Models C and D incorporating the FPD undergo overall higher equivalent strain than Models A and B (Figure 2). The higher magnitude of equivalent strains is evident and logical as the two abutment teeth are supporting a mastication load suitable for three native teeth. Thus the strains within the abutments will be significantly greater than its prebridgework counterparts as the loading condition has substantially increased. From Figure 2, the cortical strains in the freshly extracted tooth Models A and C are observed to be much lower than their native counterparts [25] due to removal of part of mastication load, suggesting that resorption may occur around the cortical ridge. The resorption is an expected outcome as upon extraction a reduction in ridge height subsequently follows [8]. Figure 5 also displays a considerable increase in strains around the apical third tooth root and root apex of the extracted tooth in Models A and C. This higher strain concentration suggests that it would be a site of bone apposition. This is a probable scenario as clinically upon extraction the process of bone healing involves the formation of bone within the extraction socket. It can also be noted that with the presence of bridgework, the strains within the mandibular bone are noticeably higher due to restoration of normal masticatory function (Figure 2).
Figure 4 relates the equivalent strains to the MES remodelling range suggested by Frost [10], where significant difference can be observed between the counterparts with or without the FPD construction. Model A suggests that resorption may occur in the mesial/distal/lingual/buccal areas of the cortical ridge, but apposition in root apex and about the root surface within the apical third. Model B indicates that resorption may appear in the mesial/lingual/buccal regions, making the buccal-lingual ridge thinner and lower. Model C (FPD) implies resorption in the mesial/lingual/buccal sites and remodelling equilibrium around distal region. Model D appears to perform best in terms of the effective strain level and shows possible occurrence of resorption on the lingual side only.
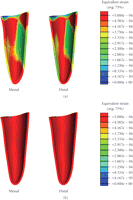
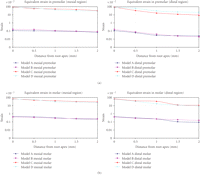
Since PDLs are of special importance to bone remodelling [43], Figures 6 and 7 provide the equivalent strain values observed within the PDLs of the premolar and molar in all the models. It is seen that the regions of bone resorption and apposition can correlate to those strains developed in the PDL. Nevertheless, the equivalent strains within the PDL are higher than those observed within the mandibular bone due to its much lower Young's modulus.
Equivalent strain contours in the premolar PDL (a) prebridgework models and (b) FPD models.
To better observe the strain distribution in PDL, Figure 8 plots the equivalent strains in the different regions versus the distance from the root apex. It is shown that in all dentitions, the highest equivalent strains are at the root apex. In addition, the equivalent strains in the prebridgework models are considerably lower than those in the FPD-models. This is a realistic outcome as the two abutments are supporting a masticatory load of three dentitions after the FPD treatments. Quantifying the response within the PDL can provide the indicators as to whether the appropriate mechanical signals are indicative to bone remodelling.
Furthermore, the anticipation of bone resorption in the extracted Models A and C can be seen as a step in the healing process of extraction as alveolar bone atrophy posttooth extraction is a well-known phenomenon [44, 45]. From Figure 3, it is noted that the FPD treatment results in the fresh extraction site experiencing a considerably higher equivalent strain, thereby somewhat better preserving the ridge height and reducing bone loss. As summarized in Table 3, considerable better apposition volumes (in percentage) can be anticipated in the bridgework Models C and D. Much greater bone volumes, 45.93% and 40.57%, respectively, in the freshly-extracted FPD and healed FPD models, reach the equilibrium of bone turn-over, compared with much higher resorption volumes of 86.20% and 86.97% in the corresponding non-FPD models. This clearly indicates the primary importance of timely FPD treatment, not only for restoring the normal masticatory function but also for maintaining bone quantity and quality.
Percentage bone volume fraction due to mastication.
The present study defines the initial biomechanical responses and possible adaptive changes within surrounding bone with or without construction of FPD. This method can supplement existing experience-based clinical predicative procedures. It is revealed that the application of an FPD leads to a noticeable alteration in normal stress/strain patterns undergone within the alveolar bone. As a consequence, the supporting bone adapts itself to such a changed functional environment. This paper suggested that the response of the bone-FPD interface (PDL and adjoining bone) to functional load is crucial to the long-term success of the prosthetic treatment. This initial status of biomechanics can be associated with specific biological cellular reactions as a consequence of biomechanical stimuli. The results provide supportive evidence that an FPD treatment in a healed extraction site would help maintain a proper equilibrium of bone turnover. Enumerating the adaptive ability of bone to multiple respective loading situations attained by using remodelling processes and bone remodelling algorithms will be our future work.
Acknowledgments
This study was supported by the Australian Research Council Discovery Project.
- Received May 26, 2009.
- Revision received July 22, 2009.
- Accepted August 7, 2009.
- © 2010 Clarice Field et al.