A caveat concerning center of resistance
- Biomechanics Group, Department of Orthodontics, Klinikum der Universität Göttingen, Göttingen, Germany
- Henning Dathe, Biomechanics Group, Department of Orthodontics, Klinikum der Universität Göttingen, Robert-Koch Str. 40, 37099 Göttingen, Germany. Email: hdathe1{at}gwdg.de
Abstract
The center of resistance is a concept in theoretical orthodontics used to describe tooth movement under loads. It is commonly used to qualitatively predict tooth movement without recourse to complex equations or simulations. We start with a survey of the historical origin of the technical term. After this, the periodontal ligament is idealized as a linear elastic suspension. The mathematical formalism of vector and tensor calculus will clarify our reasoning. We show that a point such as the center of resistance basically only exists in two dimensions or in very special symmetric spatial configurations. In three dimensions, a simple counterexample of a suspension without a center of resistance is given. A second more tooth-like example illustrates the magnitude of the effects in question in dentistry. In conclusion, the center of resistance should be replaced by a newer and wider mathematical concept, the “center of elasticity,” together with a limiting parameter, the “radius of resistance.”
Introduction
Center of resistance (CR) is a concept borrowed from the field of mechanics of rigid bodies. It was first introduced into
dentistry by G. D. Fish in 1917. Analyzing the tooth movement of a single-root tooth in the mesial plane, he argued,
Let us suppose that a horizontal force is to be applied toward the cheek. There is a point C somewhere between the apex and the gingival margin, such that if the force be applied on a line passing through that point
there will be no tipping and no rotation of the tooth about its long axis. This point may be called the center of resistance. It is undoubtedly somewhere between the gingival margin and the point half way to the apex. Of course this point may vary
with variation of the intensity of force or with change in direction of application of the force.1
Unfortunately, no references were given. He may have been referring to W. J. M. Rankine’s A manual of applied mechanics in which it was stated that for a CR of a joint,
… when stability only is in question, it is sufficient to consider the position and magnitude of the resultant of the resistance or stress exerted between two pieces of a structure at the joint where they meet, and to treat that resultant
as a single force. The point where its line of action traverses the joint is called the centre of resistance of that joint.2
But the notion of a CR preceded the development of mechanics as a formal theory. In A history of aeronautics,3 there is a cross-reference to Leonardo da Vinci, who wrote in his Treatise upon the flight of birds (refer to Figure 1, compiled between 1505 and 1506, first published in Paris in 1893), which was reprinted in English in The aeronautical annual,
When a bird which is in equilibrium throws the center of resistance of the wings behind the center of gravity, then such a
bird will descend with its head down. This bird which finds itself in equilibrium shall have the center of resistance of the
wings more forward than the bird’s center of gravity, then such a bird will fall with its tail turned to the earth.4
A reflected cutout from Leonardo da Vinci’s Codice sul volo degli uccelli. The concept ilcentro della resistentia is highlighted. The restored manuscript is stored in the Biblioteca Reale di Torino.
Theoretical mechanics as a science achieved prominence much later in the 17th century. The usefulness of this notion had, in the intervening period, been forgotten since it is mentioned neither in the history of the theory of elasticity5,6 nor in the monumental Encyklopädie der mathematischen Wissenschaften.7
However, it should be noted that the concept CR has never been rigorously defined, although it is obvious that every elastically suspended rigid body should have properties similar to those proposed by Fish. It simply assumes that for all directions of an applied force, the distributed reaction forces of the elastic suspension can be united at a single point.
In 1962, Burstone rediscovered the CR as a concept to be applied in orthodontics. He assumed that the CR should be the centroid of the elastic support, considering the strength of the fibers analogously to masses. For a model of a parabolic-shaped tooth, he derived a position of the CR at 68% of the root length.8 The usefulness of the science of mechanics in the field of orthodontics was emphasized by Haack in his publication dated 1963. He stated that
Translatory movements of teeth may be produced by application of a force at a point we shall call the center of resistance
of the supporting structure. This center of resistance, however, is not accessible for the application of such a force. The
problem then resolves itself into one of determining the magnitude and sense of a couple, which must be added to a force applied
at the bracket in order to produce a resultant which passes through the center of resistance.9
By using the simple model of a peg, Nägerl et al.10 proposed that the directions of the applied force and the resulting translation need not necessarily be the same. Further doubts about the correctness of the CR concept arose from experiments with tooth models. Nägerl et al.11 reported that
… one may anticipate, that future clinical studies will show that the center of resistance will vary with the direction in
which the tooth is to be moved.
But there is no guarantee that measurements are free from statistical or methodical errors or that a two-dimensional tooth model describes the real situation adequately.
Osipenko et al.12 proposed mathematical formulations of the CR and the center of rotation and showed that they only exist in three dimensions in specific circumstances. Although their mathematical formalism is comparable, they did not find the appropriate definition for three dimensions as did Dathe.13
The aim of the work presented here is to put these centers on a firm theoretical foundation. This article is organized as follows: first, it is shown that for all two-dimensional tooth models, there is a CR. We then present a simple example showing that in three dimensions, such a point does not exist in general. However, for sufficiently symmetric root forms, a CR does exist. The differences between the ideal and real situations can be described using a single parameter. This approach can be used to decide whether the use of the concept CR should be retained in individual situations, as a first approximation, in theoretical dentistry or not.
Since a rigid compound of elastic suspensions may have a CR, the concept is not limited to single-root teeth. Our considerations are not limited to small loads. Consequently, they should be of interest not only in relation to orthodontics but also for other contexts in dentistry with heavier loads, such as biting, tooth trauma, and related numerical simulations.
Materials and methods
We use the well-founded methods of vector and tensor calculus, which are common in technical and theoretical mechanics. A multi-linear relationship between applied loads and the location of the tooth is assumed, which is appropriate for small movements. Calculations were performed with the aid of a computer algebra system (Mathematica, Version 4; Wolfram Research Champaign, IL). The counterexample for practical illustration was constructed using the “Fischertechnik®” (Fischerwerke GmbH & Co. KG, Waldachtal, Germany) construction kit and orthodontic elastics. The reader is encouraged to repeat the experiment using his or her own methods in order to understand the phenomena.
Theoretical foundation
Two-dimensional tooth models: a warm-up for the formalism
In mechanics, statics and kinematics are the limiting cases in which either motion is reduced to displacements or forces are ignored. Since most contemporary textbooks of mechanics do not treat these aspects adequately, we will first review the most important points.
In the general two-dimensional case, a load exerted on an elastically suspended body comprises a force and a torque. From statics, it is known that every two-dimensional load can be reduced either to a pure force with line of action lying in the plane or to a pure torque perpendicular to it. The pure torque is usually introduced as a force couple, but it also corresponds to a vanishing force with a line of action, which has a nonfinite distance to the origin. From kinematics, it is known that every two-dimensional displacement may be described either as a pure rotation about an appropriate point, the pole (or center) of rotation, or if the pole tends to infinity, as a pure translation. Analogous to torque in statics, an infinitesimally small translation may be viewed as two rotations with opposite signs. Accordingly, 3 degrees of freedom are enough to describe the planar case.
Let the coordinates in two dimensions be x and y and for the direction perpendicular to them z. A generalized load comprises the force (Fx, Fy) and the torque Tz to the triple
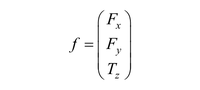
where F stands for force and T for torque. The generalized displacement is given by
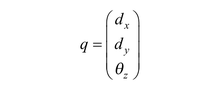
with translation (dx, dy) and rotation θz. To describe the initial movement of a tooth at rest, we assume a general linear relationship between loads and displacements as the simplest mathematical model. This is represented by the equations
which may also be viewed as a statistical regression model of an experiment that measures the displacements for given loads. The coefficients D, s, and m are the flexibilities. We have chosen different symbols for different physical units. With a dot denoting the matrix multiplication, this can be rewritten as
in which the 3 × 3 matrix is called the flexibility matrix. This may be viewed as a generalized application of Hooke’s law relating the displacement q with the load f.
If the origins of the coordinate systems for load and displacement were to lie in a presumed CR, the relationship would be expected to reduce to
since all translational and rotational effects would decouple: a pure force with a line of action through the CR will cause a pure translation and a pure torque will cause a rotation through the CR. This is the formulation of the CR in terms of the flexibility matrix.
Three-dimensional suspensions
Generalized loads and displacements are especially useful for describing the three-dimensional case. Since spatial forces, torques, translation, and rotation consist of three components, loads and displacements will have six entries, which is the appropriate number of degrees of freedom. The flexibility matrix will, in general, have 36 entries.
The main difference in changing from three to two dimensions is that a system of forces does not need to be reducible to a single force. For example, a contribution of the torque parallel to the line of action cannot be eliminated by a transformation by using another choice of system of reference. Another difference in changing from three- to two-dimensional motion is that a general movement does not need to be described as a single rotation around a special point. The general case for a spatial movement is given by a screw motion (“Chasles’ theorem”14), which has an additional translational component in the direction of the rotational axis. So, the idea of a “center of rotation” is essentially two-dimensional and is known to be not general enough to describe all cases.
The simplest example of a load that cannot be reduced to a single force is a combination of two pure forces with skewed lines of action. This is precisely the way in which the counterexample is constructed.
Results of calculations
Two-dimensional suspensions
The two vanishing components sxz and syz can be shown to be directly related to the possible translations of the origin of the loads,13 and the two vanishing components szx and szy correspond to the possible translations of the origin of the displacements. Since these origins have the same number of coefficients, the off-diagonal terms s can be eliminated by choosing appropriate origins. Note that at this stage of the exposition, two coordinate systems are used, which are not necessarily identical. If the flexibility matrix of the system is symmetrical, the origins for load and displacement would become the same. This can be justified by assuming that the work done on the periodont only depends on the load/displacement of the periodont at rest. Then, reaction forces can be derived from an elastic potential, and the flexibility matrix is symmetric. This completes the proof for the existence of a CR using a linear, two-dimensional tooth model. Understanding the flexibility matrix as the outcome of a measurement or a numerical simulation, this assumption of symmetry does not need to be true and a CR would not exist in such a case. Moreover, the singular value decomposition from linear algebra shows that the directions of translation (dx, dy) and force (Fx, Fy) need not be the same.
The three-dimensional counterexample
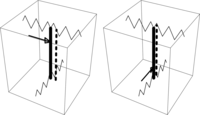
Now, the simple experiment that this suspension (see Figure 2 for a model) does not have a CR can be carried out. For reasons of symmetry, a CR is assumed in the middle of the suspended bar. To achieve a pure translation in all three directions, the lines of action would have to be (a) parallel to the long axis and central through the middle for the upward/downward direction, (b) parallel to the elastics but above the middle for the upper-left/lower-right direction, and (c) parallel to the elastics but below the middle for the lower-left/upper-right direction (Figure 3). Therefore, (a) and (b) would lead us to expect a CR in the middle of the long axis of the suspended bar above the geometric center, but for (a) and (c), it would be below it. Therefore, no point with the desired properties can be found.
The position of force-acting lines to achieve a pure translation on the model (for further details, refer to the text).
In a linearized theory, the suspension under consideration with the origin of coordinates in the geometric center would have a flexibility matrix with the structure13
in which the off-diagonal terms with e cannot be eliminated by another choice of coordinate system. This can be understood by simply counting the degrees of freedom: the off-diagonal 3 × 3 sub-matrices do have nine entries, in general, but there are only three spatial coordinates to eliminate them. The remaining three rotational degrees of freedom do not affect the CR as a geometrical point.
Special symmetries
Obviously, the counterexample does not look like a tooth root. So, the question of the circumstances under which more or less realistic root geometries would give a CR needs to be analyzed.
In his thesis, Dathe13 was able to enumerate some spatial situations in which a CR would exist. In brief, they are as follows: a suspension consisted of parts with identical CRs would have the same CR as its parts. A suspension with point symmetry would, for every partial force of the suspension acting on the suspended body in equilibrium, have a counterforce with the same line of action, but opposite sign—a CR would result. Finally, it can be shown that a linear elastic suspension with a circular or cylindrical symmetry has a CR.
Relevance to dentistry
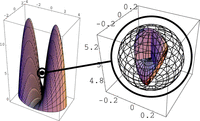
From the preceding analysis, it follows that the often discussed root of an incisor shaped like a rotational parabola would be expected to have a CR. But the more interesting question is the extent of the expected effects in real situations without a CR. So, let us now consider an over-emphasized, two-rooted tooth as a numerical example. The geometrical parameters are root length = 12.5 mm and diameter = 8 mm × 5 mm (Figure 4). The elastic properties are modulus of elasticity = 1.2 MPa, Poisson number = 0.45, and thickness of the elastic membrane = 0.2 mm. The calculations are implemented according to a new theory of suspensions composed of thin elastic layers.13 This theory uses differential geometry and computer algebra instead of finite elements and will be described in a separate report. It can be shown that the properties assigned to the CR are realized at different points. For example, the rotations resulting from a pure torque have to generalize to screw axes with base points lying on a complex surface (right part of Figure 4). But this surface is small in comparison with the root in our example: it can be inscribed to a sphere, the region of resistance, with radius of 0.32 mm. The radius of this sphere is the new parameter describing the CR as a limiting case with 0 radius: the sphere then reduces to a point.
The two-root tooth as a second example of a suspension without a CR. Figure on the right is a magnification of the circled object on the left. The wire-framed sphere is the region in which points can be found so that some properties of a CR hold true, but not at the same point. The surface on the right is that of all base points for screw axes arising from pure torques in all directions. In the case of the counterexample, the upper and lower burrs of the surface would correspond to the lines of action of the elastics.
CR: center of resistance.
Discussion
In two dimensions, the CR completely describes the situation of an elastically supported rigid body. Such models have frequently been used, and this explains the success of the concept. Since the counterexample disproves the generality of such a concept in three dimensions, the findings in theoretical models and the experimental doubts10,11 are presumably neither artifacts of the tooth model under consideration nor do they reflect experimental errors.
Since the usual definition of a CR has been too specific, a more general description has to be found. The proposed properties of the CR have to be reformulated and generalized for that purpose. Since this would no longer be the same object, we would like to introduce a new concept: the center of elasticity. Let us use the symbol E for this point.
A pure force acting through E causing a pure translation is equivalent to a vanishing torque (as a function of E) together with no rotation: 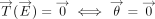 . A pure torque causing a pure rotation with axis passing through E is equivalent to no force present together with vanishing translation (as a function of E):
. A pure torque causing a pure rotation with axis passing through E is equivalent to no force present together with vanishing translation (as a function of E): 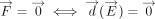 . Since only the free vector torque and translation depend on E, their lengths are minimized. This has to be equally implemented for all possible directions of the line vector force and
rotation. Since no direction is preferred, they are isotropically distributed. Therefore, with do denoting the surface element of the unit sphere, the generalizations sought are
. Since only the free vector torque and translation depend on E, their lengths are minimized. This has to be equally implemented for all possible directions of the line vector force and
rotation. Since no direction is preferred, they are isotropically distributed. Therefore, with do denoting the surface element of the unit sphere, the generalizations sought are 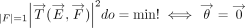 and
and 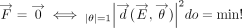 , which define the center of elasticity as the solution of a least squares problem.13 This can be formulated in terms of a flexibility matrix. For the counterexample (Figure 2), it is located in the middle of the suspended rod, as is to be expected. For the two-rooted tooth with a root length of
12.5 mm, it is located on the z-axis at 5.0011 mm, which is 67% of the root length. Note that for an arbitrary (e.g. nonsymmetrical) flexibility matrix,
these formulas define two points: one for the loads (called center of torque) and one for the displacement (center of translation), both terms were proposed by Dathe.13
, which define the center of elasticity as the solution of a least squares problem.13 This can be formulated in terms of a flexibility matrix. For the counterexample (Figure 2), it is located in the middle of the suspended rod, as is to be expected. For the two-rooted tooth with a root length of
12.5 mm, it is located on the z-axis at 5.0011 mm, which is 67% of the root length. Note that for an arbitrary (e.g. nonsymmetrical) flexibility matrix,
these formulas define two points: one for the loads (called center of torque) and one for the displacement (center of translation), both terms were proposed by Dathe.13
Let us decompose the 6 × 6 flexibility matrix into four 3 × 3 sub-matrices, so that
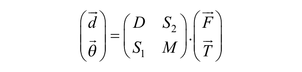
The center of translation is given by the skew-symmetric part of −S2M−1 and the center of torque by that of M−1S1 using the mapping
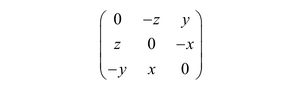
They coincide for a symmetric flexibility matrix.13 Let (w1, w2, w3) be the eigenvalues of −S2M−1 or M−1S1. Then, the radius of the region of resistance is given by the formula13
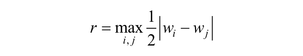
For our counterexample, the radius of resistance is half the distance of the upper and lower elastic pairs. Ciblak15 obtained comparable closed results for the center of elasticity for a symmetric matrix15 using the eigenscrew-based formulation of Lipkin and Patterson.16 Since this mathematical formalism starts with normalized screws (which have a line vector of unit length), the demand for isotropy is hardly to be found in his derivation: vanishing rotation or forces are treated as degenerate cases. Independently, they chose the same notion “center of elasticity,” which indicates that it is a good choice and that it should be accepted in dentistry. Moreover, the new name for the new concept avoids confusion with political resistance and revolts.
Viewed from the perspective of this linearized theory, the center of elasticity can be calculated from the entries of the flexibility matrix. It is an intrinsic property of the suspension, which is not affected by the applied load, as long as the displacements are small enough. Accordingly, Fish1 was incorrect in assuming the proposed dependence of the CR on the intensity of force, but maybe he sensed the influence of nonlinear elasticity. We imagine that there was no rigorous theory underlying his attempt at a definition. In the case of nonlinear elasticity, the global stiffness matrix has to be replaced by a tangential stiffness matrix. Then, a center of elasticity would exist for any center of expansion. With a change of this point, a dependence of the center of elasticity on different loads might occur.
But the frequency of occurrence of a CR under several symmetry assumptions shows that the concept should not be too hastily
withdrawn. It could indeed be replaced by the more general concept of “center of elasticity,” in which the exact demands on
loads or displacements are replaced by minimization problems, as was elucidated above.13 Fish’s attempt at definition (“no tipping and no rotation of the tooth about its long axis”) might be understood as the prerequisite
that only rotations parallel to the single force may occur. This collection of all points 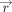 with
with 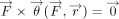 produces a surface which can be shown to be equivalent to that in Figure 4, except that it belongs to the center of translation, instead of the center of torque.13 The center of translation is the middle of the object. Taking into account the complicated shape of the surface, it is no
wonder that there have been many difficulties in understanding the mechanical behavior of elastic suspensions. It is only
with experimental consideration that one becomes aware how large these concordant surfaces of tooth or tooth assemblies are.
Taking into account our two-rooted tooth, we expect radii of the regions of resistance to be less than 1 mm. This will be
the subject of a future publication.
produces a surface which can be shown to be equivalent to that in Figure 4, except that it belongs to the center of translation, instead of the center of torque.13 The center of translation is the middle of the object. Taking into account the complicated shape of the surface, it is no
wonder that there have been many difficulties in understanding the mechanical behavior of elastic suspensions. It is only
with experimental consideration that one becomes aware how large these concordant surfaces of tooth or tooth assemblies are.
Taking into account our two-rooted tooth, we expect radii of the regions of resistance to be less than 1 mm. This will be
the subject of a future publication.
In this article, we utilized a grossly simplified model of the periodontium, that is, linear elasticity. The elastic suspension presented as counterexample does not involve such theoretical assumptions. Thus, theoretical models or numerical simulations closer to the realistic situation will result in similar problems with the CR as described in this article. Employing a more realistic model than linear elasticity usually tends to complicate the situation. The same holds for the tooth root morphology: a less symmetrical model than the one with cylindrical symmetry will tend to not even possess a CR. Clinical consequences are hardly to be expected since practical treatment in orthodontics is an iterative approach, which overcomes our predicted minor differences in reference to the ideal case.
Conclusion
The CR concept has been shown not to provide an adequate description for all situations. We present a mathematically based definition of an object, which preserves as much as possible of the desired properties of a CR. This so-called center of elasticity can be defined in terms of screw theory and does not involve assumptions on the elastic model or the symmetry of the tooth root. We hope that our definitions of the “center of elasticity” and the “radius of resistance” will facilitate further theoretical understanding of this subject.
Acknowledgments
At an early stage of this work, computing facilities of the Gesellschaft für Wissenschaftliche Datenverarbeitung Göttingen (GWDG) were used. The authors thank David A. Tigwell for writing assistance for this article and Gunther Helms for some useful comments.
Article Notes
-
Declaration of conflicting interests The authors declare that there is no conflict of interest.
-
Funding This study was supported by the German Research Foundation and the Open Access Publication Funds of the Göttingen University.
- © The Author(s) 2013