The places of mathematical practice in seventeenth century Europe are scattered geographically and socially, yet, for reasons that shall become obvious, networks of vivid communication do exist. Hence, in many respects, European mathematics constitutes a specialized field, that develops according to a relatively autonomous dynamics, which also means that it distances itself from the values of other kinds of activities. Studying the role of mathematical instruments is promising an approach to measuring these distances or proximities (by gauging the degree of autonomy), and also to understanding the dynamics of the field at that time. Two main facets of the ‘sector’ can be considered: one is the mathematical facet, where mathematical reasoning internal to the field applies, while the other facet relates to other aspects of the instrument considered as an object material, symbolical, economical. From this vantage point, the ‘sector’ resembles a hinge where two realms – mathematics and the remainder of the world – can be observed in their relation to each other. This is why the examined text may reveal something about the impact of further or lesser distances of those two realms.

The Jesuit Ignace Stafford (alias Lee or Badduley) (1599–1642) is the author of two printed works and about a dozen manuscripts extant in three different libraries in Lisbon.¹ The manuscript we will explore bears the title Arithmetica practica geometrica logarithmica and is a treatise that presents a traditional introduction to computation and to solving simple arithmetic problems.² It starts by explaining the decimal numbers and fractions, the four basic operations and extraction of roots and elevation to powers, the usual rules for commercial companies, the simple and double false position. Then follow some results concerning geometrical progressions, and the sum of finite series in geometrical progression applied to the solution of various problems about pensions and capital interest. Stafford also includes a series of trigonometric and several geometric problems, to conclude with the problems of finding arithmetical, geometrical and harmonic means or the number or magnitude of extreme and mean proportion, and the maximal harmonic proportion. As a kind of appendix he refers to the traditional methods of geodesy, the measuring by ‘visual rays’, explaining the use of pinnules mounted onto the sector. None of these seem to be original contributions by the author, and he gives repeatedly credit to the sources he follows.

The treatise is divided into two main parts: first a set of classical definitions and axioms, followed then by a series of propositions (nearly always formulated as ‘problem’) of which the solution is usually given discursively in general terms (without demonstration though) and then illustrated by various numerical examples running over several paragraphs. In some instances there are references to demonstrated propositions in a work called Trigonometria logarithmica written by the same author.³ In many ways this is a traditional kind of treatise of practical arithmetic, also with regard to the ‘picturesque’ collection of ‘practical’ problems.

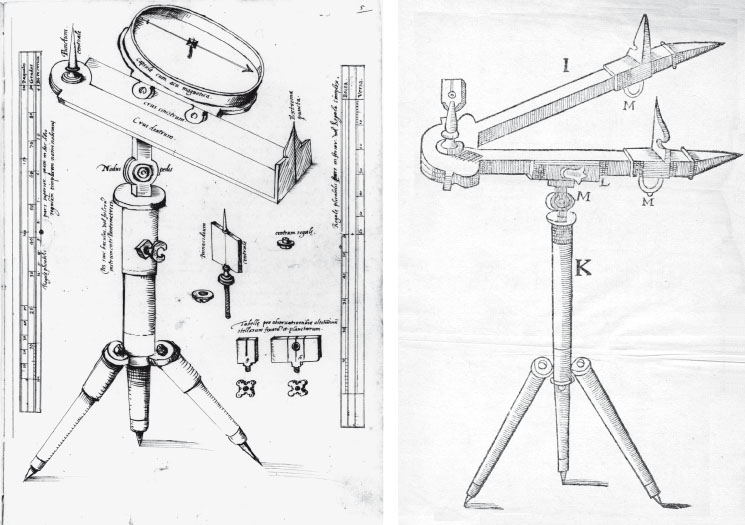
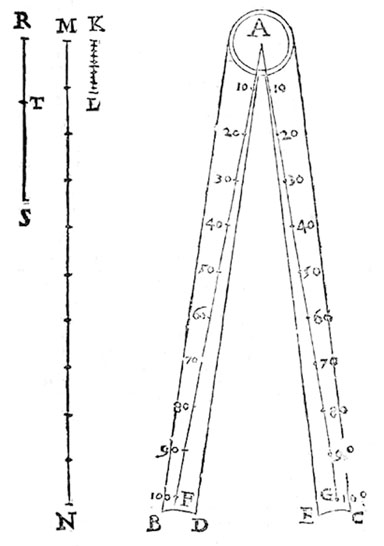
What then is special about Stafford’s Arithmetica? Throughout the treatise, Stafford invokes the use of instruments, three of them in great detail: the sector, Oughtred’s fg001 circular slide rule (proposed by William Oughtred, 1574–1660), and the cross-staff with Gunter’s line (named after Edmund Gunter, 1581–1626). In fact these instruments figure very prominently in the text: the first twenty two propositions deal with the construction, or to use Stafford’s expressions, the ‘proiecion, seccion, fabrica,’ of the instruments’ various scales.

Curiously enough in Stafford’s text, the sector is called ‘el pantometra.’ As we will now show, this particular terminology points at the circle of readers the author had in mind when he wrote up his treatise. We know that ‘pantometrum’ is a generic name given to several instruments at the time that had the particularity – according to its etymology – of combining several modes and objects of measurement, usually angle measurements.⁴ Nevertheless, the one who probably first called a sector-like instrument fg002fg003 a ‘regula pantometra’ or ‘pantomètre’ was Michiel Coignet (1549–1623).⁵ Coignet devised many variants of his ‘pantomètre’, which usually came along with its pantometric ruler, but none of these would have logarithmic scales like Gunter’s sector.

He worked as a private teacher to officers and merchants. Also, from 1596 onward, Coignet sought the patronage of Archduke Albert of Austria, who had become governor of the Spanish Netherlands and had recently arrived from Madrid. Coignet acted as an advisor during the sieges of Hulst (1596) and Ostend (1601–1604). This is how he could have linked directly to the network of Iberian officials and put the term ‘pantometra’ into circulation. To attest for the interest his ideas aroused, his manuscripts are to be found today in libraries all over Europe: at least in Prague, Paris, Oxford, Florence, Brussels, Vatican, Napels and also in Madrid although, in the latter place, none about the ‘regula pantometra’.⁶ If Stafford (who is aware of Coignet as a geometer as we will see) later takes up the name of ‘el pantometra’ although he refers explicitly to Gunter’s sector as described in the English translation De sectore & radio,⁷ this appears to be due to the fact that the people he met in Valladolid and in Lisbon were familiar with the instrument under this name, as he attests in this passage:

[…] the use of the logarithmic and geometric instruments that I wanted to describe, mainly [the use] of the gramelogia, of the pantometra, and the radio [geometrico], because these are the most important and practical that have been invented until now. And because these are the ones the persons are using, for whose sake I have taken up the present matter.⁸

[…] 3. The author of the pantometra I am considering was Edmund Gunter, lecturer of geometry at a college of the University [sic] of London, published in the year 1623, he called it ‘sector of a circle’, or simply ‘sector’ because of the similarity it bears to that shape, although I call it pantometra, in order to conserve the common designation.⁹

In his manuscript treatise about military architecture Stafford writes:

But when one executes [the solution] by the compass, or by the circles of proportion, which in an other language, and commonly are called the pantometra, and gramelogia, it is necessary to follow the indication of the geometrical analogies […].¹⁰

His argument for using the term ‘el pantometra’ is ‘para no dejar la phrasi comun’ and because ‘vulgarmente se llaman’, which hints, as to the readership he had in mind, at a group of people, Jesuits or not, very probably with links to the Habsburg court or Iberian military circles. Those would be familiar with Coignet’s manuscripts or the French publication and terminology, and hence using ‘el pantometra’ to designate the sector-like instrument. One of the few things we know about Stafford’s adolescence, is that in 1618 or 1619, at the age of nineteen, he entered the Jesuit order in Villagarcia (Galicia). He spent the years from 1620 to 1625 at the Collegio de los Ingleses San Albano in Valladolid (Castile) which aimed at preparing English exiles for missionary work in England and was under Jesuit direction. After that, his superiors sent him to Lisbon as a confessor.¹¹ Finally, he started teaching mathematics at the Jesuit Colégio de Santo Antão in Lisbon (1630–1636) on the chair of the famous ‘Aula da Esfera’ or ‘Real Academia Mathemática’.¹² In 1636, he returned to Castile. A collection of Stafford’s manuscripts on various mathematical matters are dated 1638, and the front page of these Varias obras says they were ‘unfinished because of the author’s death’. Nevertheless, according to the biographers and the Jesuit Catalogus triennalis from Rio de Janeiro, he accompanied the vice-king, Dom Jorge Mascarenhas (d.1652), Marquis of Montalvão (Monte Albano), on a trip to Brazil, in 1640.¹³ Shortly after his return to Lisbon he died, in 1642.

This means that Stafford wrote his Arithmetica with people in mind who were familiar with Coignet’s terminology and instrument ‘regula pantometra’ or ‘le pantomètre’, and belonged either to Jesuit circles in Lisbon or Valladolid, or to the entourage of the vice-king Dom Jorge.

In these circles Coignet’s works could have circulated through the Spanish network as early as 1596. A later potential link is the Jesuit mathematician Joannes della Faille (1597–1652), who was trained in Antwerp, and taught at the Jesuit college in Louvain before he went to teach and work at the Collegium Imperiale of Madrid and for Philip IV in 1629. His famous portrait by Antoon Van Dyck (1599–1641) was probably painted at the occasion of his departure to Spain and shows Della Faille sitting at a table full of mathematical instruments, among them a sector.

One of the strongest factors of autonomy of the field of mathematical knowledge is the adherence to a traditional corpus of mathematical concepts, problems, and specialized methods. During the Renaissance, as is well-known, mathematical authors maintained a conscious reference to antique authors such as Euclid, Archimedes, Apollonius etc. Among the authors of the sixteenth century, there was a clear tendency of presenting even new developments as based on their venerable classical foundations. This allegiance to classical antiquity meant, on the formal level for example, that a mathematical text would start with a set of definitions and axioms and would then be divided in a series of propositions (a format alternative to dialogue, Quaestio or other traditional forms of learned discourse). Even the structure of a single proposition is more or less determined. The Euclidean ideal of mathematical exposition maintained a conspicuous influence. So it was part of the duties of the mathematicians to restate the Euclidean definitions and axioms, and to fg004 reproduce the Euclidean ideal of mathematical exposition. On the other hand, the Renaissance mathematicians also inherited the non-Euclidean traditions: there is for instance a traditional set of problems used in treatises on practical arithmetic like those in Fibonacci or Paccioli.

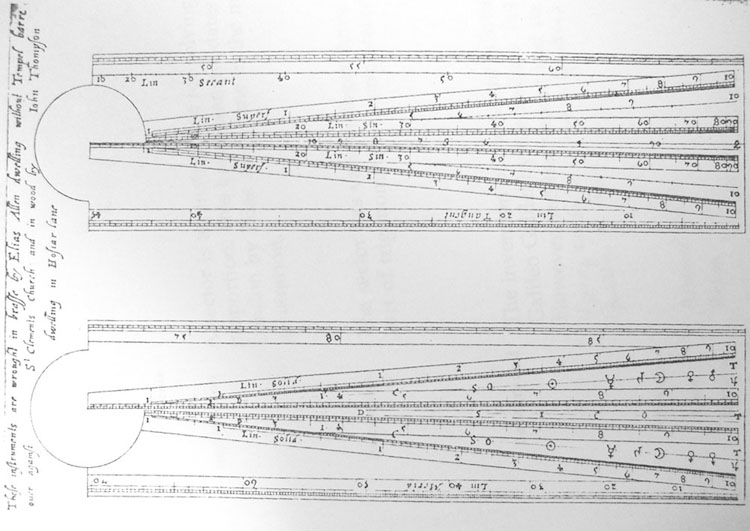
These characteristics appear combined in Stafford’s Arithmetica: As shown before, this book begins with a section with definitions, all of them classical definitions as they are to be found in book VII of the Elements or in De institutione arithmetica by Anicius M.S. Boethius (ca. 480–524). Like this latter author, he concludes the book by addressing the problem of different means and the maximally harmonic proportion, thus echoing the final paragraphs of this classic of arithmetic in the university syllabus. However, let us look now at the particular way in which Stafford explains the construction of the line of solids, which is one of the typical lines on the sector that allows the calculation of cubes and cubic roots, and hence determining two mean proportionals between two given quantities:fg007fg005

The author relies doubly on antique heritage: he uses a solution attributed to Apollonius for the geometrical construction of two mean proportional straight lines by neusis. His exposition, moreover, proceeds along the classical sequence of a geometrical proposition: exposition, construction, demonstration, and conclusion, and hence reproduces the Euclidian mode formally, too. While presenting the structure of the pantometra, in contrast with his model text on the sector by Edmund Gunter (1581–1626), the Jesuit mathematician takes care of including traditional methods and demonstrations. So one can conclude in this case that Stafford invokes traditional knowledge both formal and conceptual. What is striking in that respect, however, is the very progressive use of abbreviated notation. This is already a sign of a connection with a novel tradition who sought to introduce ‘symbolism’ into geometrical discourse.

We know that, beyond the influences from present and past, mathematical work does not emerge completely isolated even from the world outside mathematics. This is why one needs to qualify the degree of autonomy of mathematical knowledge and its development. We shall now see in the case of Stafford’s Arithmetic several ways in which content connects to historical context. Stafford’s times were marked by economic and political instability, provoked by the expanding trade routes, innovation in the production system, the rivalling monarchies of Spain, France, England and the Levant, all these exacerbated by religious disputes. Fundamentally, it was plagued by hopeless poverty, repeated crises, which resulted in repeated agrarian rebellions, attempts at institutional reforms and never ceasing wars. With respect to Lisbon, where Stafford resided, during the last decade of the union of the crowns of Spain and Portugal, elite circles conspired with the project of a renewed independence of the Portuguese kingdom. Influence of this general restlessness appears in the choice of example problems that enter the corpus of traditional problems. These examples, usually to be solved by the rule of three, reflect the world that surrounded the author Stafford:

11. A knight intends to serve at war 6 years, and finds that in 7 months and 13 days, the expenses attain 6500 [reales].¹⁴ He would like to know how much money is needed for the expenses of 6 years.¹⁵

13. A merchant bought in Lisbon 400 ells of tissue for 800 [reales], gave them to a servant for him to sell them in the Alentejo, ordering him to make a profit of 16,000 [reales] at a ratio of 5 percent. The servant took the 400 ells to Evora, and he spent 5 [reales] for each ell in tolls and portage. In Evora he sold 180 ells for 860 [reales] each; he takes the remaining 220 further to Castro Marin, and spent 8 [reales] for each ell in tolls and portage. One asks at what price the servant needs to sell these 220 ells in Castro Marin to come out straight with the profit in the tissues that his master asked him for. […] That’s how I conclude that […] he needs to sell the 220 ells for 840 in Castro Marin, cheaper than in Evora. If he found the market favourable, however, he would sell at a higher price, (of which there is no doubt) as the bachelor will imagine, and he can divert the excess profit for himself, with which he will start to enrich for hell.¹⁶

24. A very honourable inn keeper buys 210 jars of wine for 160 [reales] per jar; and in order not to lose the sale, if he sold expensive, he wants to sell the 210 jars at a base price of 120 [reales] per jar, nevertheless he wants to earn 1800 [reales], so he would like to know how many jars of water he should add to the wine so as to reach such a profit.¹⁷

6. The army of a besieged fort is 8500 men strong, but possesses victuals for 11 months. There is however no hope for assistance nor for the siege being lifted before 25 months. It is asked how many people should be retained.¹⁸

5. If 30 artisans can finish a work within 4 years, in how many years 50 [artisans] will finish it?¹⁹

9. Four captains, 6 lieutenants and 100 soldiers, when distributing a booty of 72,400 cruzados agreed that every lieutenant will get 5, every soldier 3 times as much as every captain 8.²⁰

When commenting on the different currencies with their subdivisions of coins, Stafford gives preference to the Portuguese, as he says:

Mrs. ‘Money’ although admitting greater variety in her integer and fractional numbers [compared to units of weight and volume] […] the Portuguese is doubtlessly the best of all, not only because it is the simplest, but also because it divides up into tiny parts, and comforts the poor who may, with little substance, show off thousands of coins.²¹

Another example, famous already in his time, is Stafford’s invective against the habit of using the bad ‘ordinary sea charts’ instead of one using the Mercator projection. He comments on this problem when introducing the meridian line on the sector.²² On this question, he can already cite an ancient authority: Pedro Nunes (1502–1578).²³

[…] that’s why on the ordinary chart the ratio of longitude of Friesland is double with respect to the globe, and to the true [longitude]; on the isles of Groenland and Groeland it is four times the true one because of the meridian of Friesland being double of its parallel, and [the meridian] of Groeland, and Groenland four times its parallel.

[…] I will note an example of this effect by Pedro Nunes. The distance between Lisbon and Ilha Terceira is estimated at 262 Portuguese Miles (where 17½ make 1° of a great circle).²⁴[…] that’s why the drawing of this black chart has been the most pestiferous invention that the ignorance and carelessness of our friends the mariners has brought upon navigation. Good Pedro Nunes said in his time that he knew a lot advocates of the vulgar chart, and had with them several disputes, with no effect, however. In his book on navigation, he left for them written several exhortations, invective sermons, that would have been so useful in the ignorance of his time, as you can see in [the ignorance] of our century that keeps as a heritage the errors of its ancestors.²⁵

Stafford then moves on to give an ‘historical’ account of how the technique of realizing a Mercator projection came about. One sees in this set of citations how, while introducing contemporary elements, the author also includes moral judgement, and criticizes realizations and practices in his present time world, practices contrary to mathematically guided reason. The following are the issues he apparently points out: the erroneous way of navigation (repeating Nunes’ example), the making of private profit by exploiting the market price instead of selling at the adequate price (the servant of the cloth merchant), the cheating on the product to resist the obscure forces of offer and demand (the inn keeper), the spending of life years and money on war (the knight), the misery of the poor (showing off their little substance) etc.²⁶

In addition to this non-mathematical matter intruding into Stafford’s text from the historical context one should underscore that a couple of very recent mathematical innovations make their appearance, too. There is the case, as we have seen, of the demonstration borrowed from Apollonius. Although inherited from antiquity, this and other methods for finding two mean proportionals are included in Eutocius’ commentary of Archimedes’ The Sphere and the Cylinder, a text which starts to circulate during the mathematical Renaissance in the sixteenth century. More specifically even, Stafford uses a modern, abbreviated notation. On the one hand, he adopts John Napier’s (1550–1617) notation of decimal fractions using a comma to separate integers from the fractions, on the other hand he uses Oughtred’s ‘symboles of word’s’ to note equations and analogies, and he chooses a semi-colon (;) to note a ratio.²⁷ Such notation is considered (by Oughtred and his followers) more easily intelligible than the pure discourse. Furthermore, the solutions of the traditional arithmetic problems are enriched with new methods of solution: using the logarithm tables and several other recently invented instruments: the sector, Napier’s bones, etc. are used to think about a given problem, and to execute the calculations. Was Stafford aware of Napier as a notorious protestant fanatic? If yes, the Jesuit’s respectful words for the inventor of the logarithms and the ‘rabdology’, and his enthusiastic embracing of the new methods based on them, are a sign of autonomy in the development of mathematical knowledge.

Finally, but very significantly, Stafford’s presence in the town of Lisbon was itself a product of the historical circumstances: As an effect of the confrontational policy of the English crown and the Roman church hierarchy, many English Catholics were driven into exile to catholic countries.²⁸ Consequently, these communities provided students for English colleges in several places around Europe, in particular in Spain. It is in one of these that Ignace Stafford, born in England, gets his first training: the English College of San Albano in Valladolid. Then he is sent to Lisbon, and little later started to teach at the Jesuit College of Santo Antão. The politico-religious refugee brought with him his particular education and in his case the very special commitment to practical mathematical techniques, especially those implying English instruments. In his lectures, Stafford seems to have taught their use to students of the ‘Aula da Esfera’ mainly committed to a career in nautical activities such as pilots, cartographers, and instrument-makers.²⁹ His teaching activity and his writings may have been of a certain influence, the scope of which is still to be established.

At some point, Stafford seems to acknowledge the geographically distant traditions his Arithmetica is drawing on. So we read in the ‘Appendix’ following the first twenty two propositions dedicated to the construction of the scales on the various instruments, the following consideration about the origin of the sector:

2. The first inventor of the sector, such claim the French, was Michiel Coignet; the Italian want it to be Galileo. The first of these two, who achieved the renown of a good Geometer, could accomplish and change it in a way so it looked like a new work and invention, the latter deserved the infamy of great thief of others instruments. And so neither the one nor the other will retain the honour that is due to the first inventor; because Father Clavius – much earlier than both of them – shows at the beginning of his Geometria practica the design of an instrument which he calls ‘instrument of parts’, where there are sketched out the first shapes of the sector; and over this foundation Coignet could very easily raise his building. However, he left it still very unfinished, as anyone can see, who is willing to put side by side the sector that I am considering with Coignet’s.

3. The author of the sector I am considering was Edmund Gunter, reader of geometry at a college of the University [sic] of London, published the year 1623, he called it ‘sector of a circle’, or simply ‘sector’ because of the similarity it has with that shape, although I call it pantometra, in order to conserve the common designation.³⁰

Stafford attributes the invention of the sector to Christophorus Clavius (1538–1612) as having laid the foundation.³¹ Apparently he considered the addition of the whole variety of fg006 scales as a development less important than the fundamental structure of the instrument. Nevertheless, it seems also that he attributes glory as a function of religious affinity and reverence. This said, we have seen that the technical contributions are not actually rejected, even when they originate from a religious opponent, e.g. Napier. Still, some resentment towards Galileo Galilei (1564–1642) is expressed. Stafford’s opinion seems strongly influenced by his affinities to Clavius’ religious position and Galileo’s renown of heterodoxy. So, are we then to assume that in questions of attribution of an invention some relevant arguments lie, strictly speaking, outside the field boundaries?

A text about the design and use of a sector implies the bridging between the spheres of ‘mathematical concepts’ and ‘materially crafted’ instruments. Stafford’s text gives a few hints about the difficulties of bridging this gap. Admittedly, there are very few of such passages where we could speak of a conscious perception of the distance between abstract reason­ing and instrumental operation.

The first I could locate is rather trivial. It is included in problem number 3, where Stafford sets out to explain the construction of the scales of tangents on the sector. These scales are usually divided into 100 or 1000 parts, he says, while the radius assumed in the tangent tables is 10 000 000, hence the necessity of rounding the numbers found in the tables. This shows that Stafford is well aware of the compromise when you pass from using the tables to using the instrument.

Proposition 3; Problem 3: How to accomplish the dividing of the tangent and secant lines on the sector.

[…] of the number that corresponds in the tangent table to the required arc, five figures on the right hand side are removed, given that the radius is 10. 000 000, so that the radius be 100, equal in number to the subdivisions of radius AB;

[…] 5. Note that when, after excluding the five figures of any tangent or secant of the tables, the last of the excluded on the left hand side is 5, the first on the right hand side of those that will remain, shall be increased on the radius by a half, and by one entire unity if the last of the excluded is 8, or 9.³²

A few pages further in the text, the author draws the attention to another condition that depends on the actual size of the material instrument. If the latter is of medium size, acknowledges Stafford, it is in fact materially impossible to engrave distinctly the thousandth in the scale of solids:

7. The constructing of the scale of solids can be performed in any of these three ways, […] although if the sector is of medium length, it will be impossible to distinctly express all the unequal thousandth parts.³³

Thus, the author is well aware of the distance lying between his theoretical explanation of how to design an instrument and the actual material manufacture.

Eventually, Stafford manifests awareness of still another kind of distance: the one left behind by travelling knowledge while it is handed down from the first text that would describe the instrument (the source) down to his own text. He writes at the end of his ‘Appendix’:

Up to this point the authors [Gunter and Oughtred] of these instruments teach us their design and construction. If [they did it] better than [myself in] the preceding propositions, then I have struggled in vain: and if not, I wish to heal the illusion of those curious people who are only satisfied with what they expect to be better at the source, than in the river: and it is not always like this because often the water at the source is crude and too thin, and flowing down it acquires perfections, like the Tajo river by the gold sands with which it becomes loaded.³⁴

He compares the knowledge about the sector to a river and states the problem first in the form of a paradox: People would usually think that it is better to drink water at the source rather than from the river, i.e. better to read Gunter than Stafford. But, in this case – meaning his own work where, on the construction of the scales of the sector, he had added detailed accounts, which were actually missing in Gunter’s account – he thinks that the knowledge about the instrument has grown better and richer in his own text. This phenom­enon compares to the Tajo river, that is known to carry gold sand at the end of its mean­dering when it reaches the estuary at Lisbon.

From this we may conclude, that Stafford acknowledges that circulation does not leave knowledge unaltered: on the contrary, he argues that - running down from its source – the text has been enriched by valuable additional explanations. These additions, as we have mentioned, are theoretical or foundational explanations for the major part.

1. Bridging distance between two textual genres

By way of conclusion, one could ask: how do the described kinds of distance affect the circulation of knowledge. Stafford uses the mathematical knowledge and the know-how to design the mathematical instrument coming from the writings of their inventors, makers, publishers. As far as the sector is concerned, he refers to Edmund Gunter’s De sectore & radio. Nevertheless, his treatise is not a manual for the practical production of the instrument, even if he describes the geometrical construction of its scales. As a mathematics teacher, he seems to use the instruments to enrich the bulk of exercises in a book on practical arithmetic or to use it as a tool to visualize the relations of the terms entering a computation. By doing so, he not only bridges a geographical distance (by introducing several English instruments in Portugal), but he brings together two different genres. While the literature he is using derives from the, then very popular, genre of ‘De usu & fabrica’ books,³⁵ we clearly see that Stafford’s Arithmetica practica geometrica logarithmica is not of the same genre, it is instead, in view of its title, content and organization, a kind of Summa of elementary arithmetic: there is nearly no hint at the manufacture of the instruments, neither at their materiality nor their size, neither are there any templates ready to be used (unless they were separated from the ms. and lost). The instruments that the author imports from that other genre come to complete the picture and to form a new conception of what one has to consider now a ‘practical arithmetic,’ namely computing and solving problems by the methods old and new, including the mechanical ones. We could envision this procedure as a kind of re-embedding of knowledge contained in ‘De fabrica et usu’ books into an encyclopaedic textbook of practical arithmetic.

2. Increasing distance again: theory content as a measure for distance

Stafford’s Arithmetica clearly is not a ‘De fabrica & usu’ book and the author himself has pointed to one of the distinguishing features: the books he refers to lacked a detailed and theoretically founded description of the construction of the scales of the instruments. This means that the author distances his work from those of the instrument inventors and makers. He is intentionally increasing this distance by loading his discourse with foundational knowledge: we have seen the example of the lines of solids where he hooks up to the antique tradition through Apollonius’ method of cube duplication. This is perhaps another sign of the relative autonomy: the requirement for mathematical discourse to include the theoretical background knowledge. The distance may increase further considering the fact that Stafford uses an abbreviated mathematical notation for proportions and equations, a feature that must have appeared as quite ‘esoteric’ to the average student around 1630, who would be used to the first six books of the Elements.

This increased distance between two traditions – the one of ‘De usu & fabrica’ and the one of arithmetic textbooks – nevertheless contributes to the circulation of instrument knowledge in a context where it would not necessarily be expected. This double move of bringing two genres together but immediately enhancing their distance again, clearly ensures a wider circulation if not of the instruments themselves so at least of the knowledge about them.