Strategizing the Clone Wars: Pharmacological Control of Cellular Sensitivity to Radiation

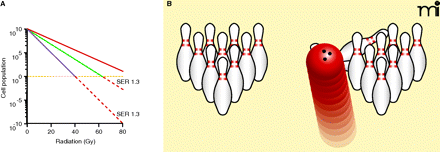
Quantifying radiosensitization and the therapeutic challenge. (A) A typical macroscopic tumor may have over 1010 cells and if even a single cell remains after treatment, the tumor may relapse. Although the benefit of a radiosensitizer may be small on any given day, the compounded effect of cell death over thirty or more days of radiation is quite large. In this example, each 2-Gy dose of radiation, administered to a tumor originally consisting of 1010 cells, kills 40% of the tumor cell population (red line). Radiosensitizers effectively decrease the dose of radiation needed to achieve a given percentage of cell death; the ratio of the required radiation dose in the absence of radiosensitizer to the (lowered) dose required in the presence of radiosensitizer is known as the sensitizer enhancement ratio (SER). Agents with SERs of 1.3 (green) and 1.7 (purple) are also modeled. Conceptually, the graph shows that a “cure” will require sufficient irradiation to decrease the number of surviving tumor cells to less than 100 (yellow horizontal line). (B) To further illustrate the difficulty of killing 10 log units of cells, imagine each bowling pin as a log of cells, with 10 bowling pins collectively representing 1010 cells. A therapy that removes 99% such a population of tumor cells (i.e., a reduction of 2 log units) is the equivalent of removing 2 pins—not a very successful frame for a bowler and certainly not a very successful therapy for a patient.