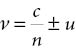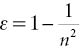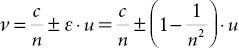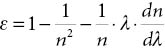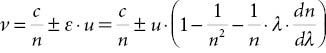Einstein in Amsterdam
Op 14 september 2015 slaagde de Laser Interferometer Gravitational-Wave Observatory (LIGO) er voor het eerst in gravitatiegolven te detecteren, waarvan het bestaan honderd jaar eerder al door Einsteins algemene relativiteitstheorie was voorspeld. De twee opstellingen die de golven waarnamen (één in Washington en één in Louisiana) bestonden uit twee gigantische interferometers, met ‘armen’ van vier kilometer lang. Slechts met deze techniek kan de benodigde, onwaarschijnlijke precisie worden bereikt: het apparaat is in staat een contractie van zijn arm van een duizendste van een diameter van een proton vast te stellen (10–18 m). Minder bekend is dat Einsteins ideeën al veel eerder op interferometrische wijze zijn getest. Al in de jaren waarin hij Nederland regelmatig bezocht, nam Einstein persoonlijk poolshoogte van de verfijnde wijze waarop een flegmatieke, Amsterdamse experimentator gegevens ter ondersteuning van zijn speciale relativiteitstheorie aandroeg met behulp van interferometrische opstellingen (zij het dat deze metingen geen onomstotelijk bewijs leverden, zoals wij hieronder zullen betogen).
Einsteins bezoek aan het Amsterdamse laboratorium van Pieter Zeeman (1865–1943) – want om hem gaat is – is vastgelegd op een foto, de enige foto trouwens waarop beide heren samen figureren (fig. 1). De derde persoon is Paul Ehrenfest (1880–1933). Getuige een briefje dat Einstein vanuit huize Ehrenfest aan zijn geliefde (tevens nicht en achternicht) Elsa Einstein (1876–1936) schreef,1 voltrok dit bezoek zich op 28 of 29 mei 1920. Het was tijdens een Amsterdams uitstapje, waarbij ook een bezoek aan de Wis- en Natuurkundige Afdeling van de Koninklijke Akademie der Wetenschappen op het programma stond, waarvan Zeeman trouwens de secretaris was. Einstein was net tot buitenlands lid van de Akademie benoemd, zoals hij Elsa liet weten. ‘[N]ichts erzählen damit nichts in die Zeitung kommt’, voegde Einstein daar nog aan toe, die zijn buik meer dan vol had van de extreme reacties die zijn doen en laten in het hypernerveuze Berlijn teweegbracht, zelfs kennelijk als het ging om een weinig spectaculair eerbetoon van de nationale wetenschapsorganisatie in een klein buurland.2 In Zeemans lab ging het er een stuk rustiger aan toe – zolang Zeeman maar niet het apparaat in werking stelde dat de reden vormde voor het bezoek. Van dit apparaat is op de foto rechts onderin net een stukje te zien. Het betreft een klein deel van de opstelling waarmee Zeeman de lichtsnelheid in bewegende staven glas en kwarts mat. Einstein was al bij een eerder bezoek (oktober/november 1919) van plan geweest om ‘Ihre feine experimentelle Anordnung’ te komen bekijken, zoals hij Zeeman later had geschreven, maar dat was toen helaas niet gelukt.3 Nu kon hij alsnog met eigen ogen zien hoe Zeeman zijn relativiteitstheorie op de experimentele pijnbank legde. De opstelling was een vervolgproef van een serie experimenten die Zeeman een paar jaar daarvoor had gedaan. Ging het toen om de lichtsnelheid in stromend water, dit keer ging het om de lichtsnelheid in bewegende, transparante, vaste stoffen.
Einstein en Ehrenfest op bezoek aan het laboratorium van Zeeman te Amsterdam in mei 1920 (Foto Museum Boerhaave)
Einstein staat centraal op de foto. Zeeman staat, typerend, enigszins verscholen achter zijn apparaten, terwijl Paul Ehrenfest, eveneens typerend, ogenschijnlijk zoekend naar contact, zijn lichaam naar de beide anderen toe draait. Zeeman en Einstein kijken ietwat onthecht in de camera. Beide heren hadden eigenlijk ook weinig gemeen. Zeeman had niet Kamerlingh Onnes’ uitgekookte opportunisme om Einsteins ideeënrijkdom te benutten voor zijn eigen onderzoeksprogramma; evenmin bezat hij Lorentz’ intellectuele capaciteiten om Einsteins ideeën op een hoger plan te tillen, en Zeeman bezat al helemaal niet Ehrenfests zielsverwantschap. Einsteins grote doel was om alle delen der fysica in algemeen geldende wetten onder te brengen. Zeeman trok juist de natuur in stukjes uiteen om die met almaar grotere precisie en verschillende benaderingen aan onderzoek te onderwerpen. Zeeman zoomde in, Einstein zoomde uit – nog een wonder dat ze samen scherp op de foto staan. Alleen achteraf kan worden vastgesteld dat ze op het moment van de foto wel degelijk iets gemeen hadden: ze stonden allebei op een kruispunt van hun carrière. Zo op het oog is Einstein niet buitengewoon onder de indruk van wat hij zag. Dat was niet zonder reden, zoals we zullen betogen.
Zeeman voerde zijn eerste serie proeven, naar de lichtsnelheid in vloeibare media (ofwel water) uit tussen 1914 en 1917, de serie experimenten in vaste media (kwarts en glas) volgden tussen 1919 en 1922. Belangrijke delen van de oorspronkelijke opstellingen bevinden zich nu in de collectie van Museum Boerhaave. Deze objecten leiden ons door het verhaal. Maar eerst gaan we vluchtig kennismaken met Zeeman en geven we een korte voorgeschiedenis van het interferometrische onderzoek.
Einstein en Zeeman
Toen Ehrenfest in 1919 Einstein ertoe probeerde te bewegen om Leids hoogleraar te worden, noemde hij Zeeman als een van de inspirerende Nederlandse fysici in wiens nabijheid hij zou komen te verkeren (behalve Zeeman en hemzelf noemde Ehrenfest: Hendrik Lorentz (1853–1928), Willem de Sitter (1872–1934), Johannes Kuenen (1866–1922), Johannes Droste (1886–1963), Adriaan Fokker (1887–1972), Willem Julius (1860–1925), Jan Burgers (1895–1981), Wander de Haas (1878–1960) en diens vrouw Geertruida de Haas-Lorentz (1885–1973). Zeeman behoorde kennelijk tot het elitaire kringetje vakgenoten van wie Ehrenfest aannam dat ze Einstein aanspraken.4
Einstein kon ook als geen ander Zeemans experimentele kwaliteiten op waarde schatten. Diverse recente studies tonen de opvallende affiniteit die het icoon van de theoretische fysica had met de praktische kanten van het vak.5 Als zoon van de eigenaar van een elektrotechnische firma, Einstein und Cie, groeide hij op tussen dynamo’s, booglampen en elektriciteitsmeters – het was een van de kleinere firma’s die München, en andere Duitse steden, het tijdperk van de elektrotechniek binnenloodsten. Einstein overwoog zelfs een carrière als ingenieur. Zijn ware bestemming bleek elders te liggen, maar gedurende zijn hele leven bleef hij in de weer als experimentator en uitvinder van een bonte diversiteit aan noviteiten – van koelkasten tot aan een opmaakspiegel. Niet bepaald al zijn vindingen vonden weerklank. Neem zijn potentiaalmultiplicator, een apparaat om heel kleine elektrische stroompjes te meten – dat door Einstein steevast zijn Maschinchen (machientje) werd genoemd. Van dit prijzige, maar ontoereikende apparaat was nota bene Pieter Zeeman een van de schaarse afnemers.6 Einstein wist dus wat hij te zien kreeg in Zeemans lab, ook al omdat hij meer dan uitstekend op de hoogte was van de voorgeschiedenis van het experiment, zoals Zeeman een jaar daarvoor, een tikje beschamend, had moeten vaststellen.
Zeeman, veertien jaar ouder dan Einstein, groeide op in een pastoralere omgeving dan het mondaine München waar Einstein de eerste elektrische lampen zag oplichten. Zeemans vader was dominee in het plaatsje Zonnemaire op Schouwen-Duiveland. In Zeemans vroege jeugd verrezen er nog een nieuwe kerk en een korenmolen. Al vroeg manifesteerde zich bij Pieter de neiging om de (zowel dode als levende natuur) met grote nauwgezetheid te observeren. Eens lag hij urenlang op een schuurdak om het Noorderlicht te bestuderen.7 Na de HBS volgde een studie natuurkunde in Leiden, bij Lorentz en Heike Kamerlingh Onnes (1853–1926). Als assistent van laatstgenoemde deed Zeeman de ontdekking die hem wereldberoemd maakte: het Zeemaneffect, de splitsing van de spectraallijnen uitgezonden door een verhit preparaat wanneer dit in een magneetveld wordt geplaatst. Hoewel het Zeemaneffect aanvankelijk als een glansrijke bevestiging van Lorentz’ elektronentheorie werd gezien (beide heren deelden de Nobelprijs van 1902), bleek de klassieke fysica toch niet in staat te zijn de subtiliteiten van de splitsingspatronen te verklaren. De verklaring van het Zeemaneffect werd in de cruciale jaren 1920 een lakmoesproef voor iedere kandidaat-theorie voor een kwantummechanische verklaring van het atoom.8
Kort na zijn ontdekking werd Zeeman ingelijfd door de Universiteit van Amsterdam, eerst als lector, daarna als professor, als collega onder meer van Johannes Diderik van der Waals (1837–1923). Hij vervolgde er zijn magneto-optische onderzoek, dat echter in toenemende mate gefrustreerd werd door trillingen en ruimtetekort in het Amsterdamse Natuurkundig Laboratorium. Handig gebruikmakend van prestigieuze aanbiedingen van buitenlandse universiteiten, weekte Zeeman een toezegging los voor een nieuw laboratorium. Om de periode tot de nieuwbouw te overbruggen startte hij een nieuwe reeks onderzoekingen die robuuster was dan het delicate testen van het Zeemaneffect: de bepaling van de lichtsnelheid in bewegende transparante media.9
Zeeman werd geroemd om zijn nauwgezetheid, en meer nog om de onverstoorbare volharding waarmee hij de natuur haar geheimen trachtte te ontfutselen – de wiskundige Luitzen E.J. Brouwer (1881–1966) noemde hem ‘een Brahmaan der wetenschap’.10 Vaak haalde Zeeman inspiratie voor onderzoeksideeën uit de geschiedenis van zijn vakgebied. Dit was ook nu het geval.
Meesleping11
De zogeheten optica van bewegende lichamen behoorde tot de meest fundamentele delen van de negentiende-eeuwse fysica. Ze had de opmaat gevormd voor Einsteins speciale relativiteitstheorie uit 1905, en was ook relevant voor Lorentz’ voorafgaande ‘elektronentheorie’. De centrale vraag was wat er gebeurt met de lichtsnelheid wanneer een lichtstraal zich voorplant door een medium dat zelf in beweging is. De vraag was al honderd jaar actueel. In 1810 had François Arago (1786–1853) geprobeerd variaties in de brekingshoek vast te stellen van licht dat van sterren afkomstig was. Immers omdat de aarde in zijn baan rond de zon beweegt, zou er ieder halfjaar verschil moeten zitten in de snelheid van het van zo’n ster invallende licht. Arago liet dit licht breken in een prisma dat aan het oculair van een telescoopbuis was bevestigd. Hij slaagde er echter niet in een afwijking vast te stellen voor de brekingswet van Snellius. Dit was een hoogst verwarrend resultaat, tot Augustin Fresnel (1788–1827) met een oplossing kwam. Diens idee was dat de dichtheid van ether in materie, zoals het glas van een prisma, iets groter was dan in vacuüm. Dit zou het optreden van breking verklaren. Als een object bewoog werd het surplus aan ether meegesleept, op zodanige wijze dat de verwachte afwijking precies werd gecompenseerd. In het ‘normale’ geval, zonder meesleping, zou een stilstaande waarnemer de volgende lichtsnelheid v in een bewegend medium vaststellen:
Waarbij c/n de lichtsnelheid in het medium met brekingsindex n is; u is de snelheid van het medium ten opzichte van de waarnemer. Ter verdiscontering van de meesleping van de ether, waarvan de mate verondersteld werd af te hangen van de brekingsindex, moest nu een term worden toegevoegd, de meeslepingscoëfficiënt van Fresnel (ɛ), waarvoor bij benadering zou gelden:
Gecombineerd leverde dit de volgende formule op voor de lichtsnelheid in een bewegend medium:
Hoewel deze oplossing mathematisch bevredigend was – voldoende in elk geval voor Fresnel en de meeste beijveraars voor de golftheorie van licht – bleef de fysische verklaring onduidelijk en gekunsteld. Naast Fresnels hypothese van gedeeltelijke meesleping bestonden er rond 1850 twee rivaliserende theorieën, ten eerste die van volledige meesleping – de aarde sleept in zijn beweging álle ether in zijn nabijheid mee – en ten tweede één van een stationaire ether (zonder meesleping).
Om aan alle verwarring een einde te maken bedacht Hippolite Fizeau (1819–1896) een experimentum crucis (al noemde hij dit zelf niet zo). Fizeau bouwde een opstelling die Zeeman in hoofdzaak zou kopiëren, met een buizenstelsel waardoor water stroomde (zie de bijlage). Een lichtbundel werd in tweeën gesplitst, waarna het ene deel met de waterstroom mee door de buizen werd gestuurd, en het andere juist tegen de stroom in. Na het traject door de buizen te hebben afgelegd kwamen de lichtstralen weer samen. Door het ontstane faseverschil tussen de bundels ontstond daar een interferentiepatroon. De verschuiving in het interferentiepatroon die optrad wanneer het aanvankelijk stilstaande water ging stromen, verraadde of – en zo ja in welke mate – de lichtsnelheid beïnvloed was door de richting van de waterstroom (zie ook de bijlage). Fizeau vond inderdaad een verschuiving, en de grootte daarvan toonde binnen de meetnauwkeurigheid vrij overtuigend het gelijk van Fresnels formule aan.12 Ondertussen bleef het mechanisme achter Fresnels hypothese van de gedeeltelijke meesleping in nevelen gehuld (net als trouwens dat van de ether in het algemeen), en dit werd er niet beter op toen het befaamde Michelson-Morley experiment in 1887 al even overtuigend geen enkele ‘etherwind’ waarnam, wat een volledige meesleping suggeerde. Om de verwarring compleet te maken duidde de aberratie van het sterlicht, zoals dat sinds de achttiende eeuw werd waargenomen, juist op een stationaire ether.
Dit was de stand van zaken toen Lorentz, en vervolgens Einstein, ten tonele verschenen. Lorentz verklaarde het nulresultaat van het Michelson-Morley experiment door een contractie te veronderstellen in de armen van de interferometer, die de verwachte gevolgen van de etherwind voor de lichtsnelheid precies teniet deed.13 Deze visie raakte snel overvleugeld door Einsteins speciale relativiteitstheorie waarbij al deze effecten eenvoudig uit zijn postulaten voortvloeiden.
Het was niettemin Lorentz die zich realiseerde dat de brekingsindex golflengte-afhankelijk moest zijn. Hij voegde aan Fresnels coëfficiënt een ‘dispersieterm’ toe om hiervan rekenschap te geven. Met λ als symbool voor de golflengte van het licht werd de meeslepingscoëfficiënt van Fresnel zodoende gelijk aan:
Zodat de formule voor de lichtsnelheid in een bewegend medium te schrijven viel als:
Binnen het raamwerk van de ethertheorie viel dit resultaat lastig fysisch te interpreteren: de hoeveelheid meegesleepte ether zou nu afhangen van de kleur van het licht.14 Max von Laue (1879–1960) leidde in 1907 Fresnels coëfficiënt, mét dispersieterm, rechtstreeks af uit de relativistische formules voor het optellen van snelheden. Op 1 december 1911 schreef Pieter Zeeman dezelfde Von Laue over een voornemen om Fizeaus experiment te herhalen en zo experimenteel de theoretische waarde voor ɛ te toetsen. Von Laue reageerde per kerende post en ‘mit grossem Freude’. Het zou ‘von fundamentaler Bedeutung für die Optik der bewegten Körper’ zijn wanneer theorie en experiment op één lijn werden gebracht.15 Daarbij was er niet alleen het probleem dat de grootte van de dispersieterm moest worden gemeten. Wat ook om opheldering schreeuwde was dat wanneer men de dispersieterm in acht nam, een aangepaste versie van Fizeaus experiment door Michelson en Morley uit 1886 een slechter resultaat gaf dan Fizeaus oorspronkelijke proef (zie de bijlage). Aan deze onbevredigende situatie wilde Zeeman een einde maken. De dispersieterm was kwantitatief maar een klein effect, maar als iemand dit varkentje kon wassen, dan was hij het wel.
Water
Zeeman leert men kennen door zijn apparaten. De aantekeningen van zijn experimenten wemelen van de berekeningen en metingen die hem volledige controle moesten geven over materialen en opstellingen.16 Er wordt aangepast, bijgesteld en opnieuw gepoogd. We vinden correspondentie met leveranciers van instrumenten en andere hulpmiddelen; hier en daar duikt een uittreksel van een relevante publicatie op, afgewisseld door eindeloze rijen meetgegevens en kladversies van artikelen die zowel in het Nederlands als in het Engels verschenen in de Verslagen en Proceedings van de afdeling Natuurkunde van de Koninklijke Akademie van Wetenschappen.17
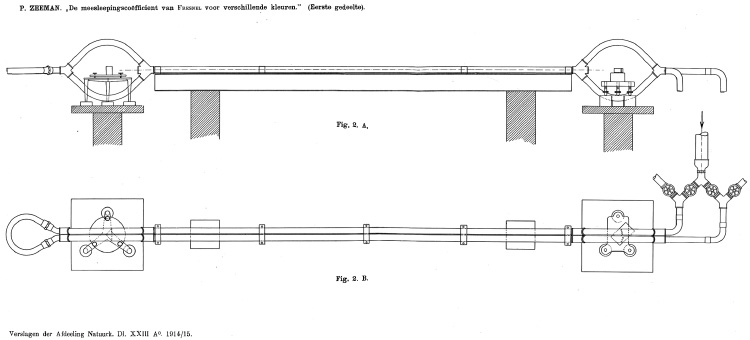
Van Zeemans opstellingen – grotendeels gemaakt door de instrumentmaker Jacobus van der Zwaal (1888–1965) – resteren drie kale buizensets (fig. 2). Van de planparallelle glasplaten (gemaakt door de Engelse firma Adam Hilger Ltd) is geen spoor meer te bekennen, evenmin als van de overige optica, de kwiklamp en de centrifugaalpomp die het water met 20 meter per seconde door de buizen joeg. Een set met kleine en dunne pijpen, 40 mm middellijn en in totaal zes meter lang, was Zeemans aanvankelijke opstelling.18 Een lichtbundel werd op de wijze van Michelson en Morley in tweeën gesplitst door hem te laten invallen op een halfdoorlatende spiegel. Een deel van het licht werd weerkaatst, het andere deel doorgelaten. De twee resulterende bundels doorliepen in tegengestelde richting het buizenstelsel; een dubbel prisma zorgde aan het uiteinde voor de omkering. Terug bij het beginpunt interfereerden de bundels in het brandvlak van een lens. Het interferentiepatroon van het voor het blote oog niet-zichtbare violette licht werd vastgelegd op een fotografische plaat. Daarvoor moest de proef enkele minuten duren.
Zeemans opstelling voor het meten van de lichtsnelheid in stromend water. Uit: KNAW Proceedings 17-I (1914)
Zeemans eerste proef leverde het probleem op dat de interferentiestrepen niet constant op dezelfde plaats bleven. Ook een tweede opstelling met grotere en wijdere buizen bood geen soelaas. Pas een derde inrichting, nog een slag groter, gaf een stabiel beeld.19 Nadat Zeeman een fotografische afbeelding had verkregen, maakte hij een volgende opname bij een omgekeerde waterstroom. De verplaatsing van de interferentiestrepen die hierbij optrad, vormde, samen met de waterdruk, waaruit de stroomsnelheid te herleiden was, de basis voor de berekening van de meeslepingscoëfficiënt.20 Behalve de gekannibaliseerde restanten van de ooit zo met zorg opgebouwde meetapparaten bevat de collectie van Museum Boerhaave nog een ander object: een oogvormig stuk buis met een venstertje, gemonteerd op een plank (fig. 3). Weliswaar is dit object geen artefact van een wetenschappelijke doorbraak van historische proporties, maar het biedt wel een prachtige blik op Zeemans zo vaak bewierookte experimentele vasthoudendheid. Zeeman gebruikte het om de snelheidsverdeling en stroomrichting van het water nauwkeurig te onderzoeken. Hij had ondervonden dat de snelheidsverdeling van het water in de buizen niet overeenstemde met wat ingenieurs-theoretisch werd voorgeschreven. De snelheidsafname van het midden naar de randen van de buis was duidelijk minder dan op grond van theoretische overwegingen mocht worden verwacht.
Zeemans opstelling voor onderzoek naar stromingen en stroomsnelheden in de buizen, vervaardigd door de instrumentmaker Jacobus van der Zwaal. (Museum Boerhaave V21783)
Aan het oogvormige hulpstuk was een doorzichtige buis gekoppeld om het stromende water te kunnen bekijken. De stroming werd zichtbaar gemaakt door er luchtbelletjes in te pompen. Door het venstertje kreeg Zeeman de stroming in beeld vlakbij de splitsing. Hij nam waar dat het water in de binnenbocht van de splitsing stilviel. Dit stukje moest daardoor in de berekeningen niet worden meegenomen in de lengte van het buizenstelsel, die iets minder besloeg dan de gehele lengte tussen de uiteinden.21 Voor Zeeman leek de weg ernaar toe haast even bevredigend als de resultaten zelf, maar laten we deze niet uit het oog verliezen. Zeeman stelde uiteindelijk voor vier verschillende golflengten de verschuiving van de interferentiebanden vast en berekende daaruit hun meeslepingscoëfficiënt. Zeeman zette de gemeten waarden af tegen de waarden die uit zowel Fresnels formule, als die van Lorentz rolde. De resultaten in de tabel tonen duidelijk een overeenstemming met Lorentz’ dispersieterm.22
| λ (ängstrom) | 45 pt | Lorentz coef. | exp. waarde |
|---|---|---|---|
| 4500 | 0,443 | 0,464 | 0,465 |
| 4580 | 0,442 | 0,463 | 0,463 |
| 5461 | 0,439 | 0,454 | 0,451 |
| 6870 | 0,435 | 0,447 | 0,445 |
Zeeman liet het niet na om Einstein zijn resultaten te sturen. Die reageerde verheugd dat nu ‘eine bisher unangenehm fühlbare Lücke’ was opgevuld: ‘Ich kann mir denken, wie schwierig es war, eine so hohe Präzision so erreichen!’.23 Hier spreekt de fijnproever. Zeeman zal in het compliment een aanmoediging hebben gezien om het huzarenstukje nog eens dunnetjes over te doen.
Kwarts en glas
Uit de paperassen over de experimenten in vaste media rijzen nieuwe stemmen op: die van de assistenten. Meest prominent is Auda Snethlage (1888–1942), die al eerder bij Johannes Diderik van der Waals jr. (1873–1971) was gepromoveerd op een onderwerp uit de moleculaire fysica.24 Behalve over berekeningen ontfermde zij zich over vertalingen en drukproeven van artikelen. Ook tijdens een verblijf bij Martin Knudsen (1871–1941) in Kopenhagen vond ze nog de gelegenheid om Zeeman correcties van drukproeven door te sturen, waarbij ze en passant uitgebreid haar beklag deed over haar gastheer, een monomane fysicus wiens belangstelling zich niet verder uitstrekte dan tot zijn eigen onderzoek. Hij was volstrekt niet genegen haar ‘zelfstandig werk’ te laten uitvoeren.25 Het feit dat Snethlage een assistentschap bij Zeeman aanvaardde toont haar wetenschappelijke motivatie. Academische carrières waren voor vrouwen echter nog niet weggelegd. Snethlage zou later nog aan de weg timmeren als vertaalster Noors.
Een andere assistent, Gerard Cornelis Dibbetz brak zich het hoofd over de snelheidsmeting bij de experimenten, de derde, Willem de Groot, heeft later met Cornelis Jan Bakker, een latere student van Zeeman met wél een mooie wetenschappelijke toekomst in het verschiet, een mooi biografisch artikel over Zeeman geschreven.26 De Groot moet een praktische geest zijn geweest. Tijdens zijn promotie memoreerde Zeeman ‘…hoe gij het waart, die door een kunstige verbinding van touwtjes en koperen schroeven assistentie bij een deel der proeven overbodig wist te maken, en op grote afstand fijne draaiingen van uw zitplaats uit wist te bewerken’.27 Zeeman gunde alle drie het co-auteurschap bij minstens één van de publicaties.
De proeven in vaste stoffen – waarvan het apparaat, met staven en al, in goede staat behouden is (fig. 4) – stelden Zeeman voor geheel nieuwe technische uitdagingen. In plaats van door stromend water moest het licht nu door een twee meter lange, transparante staaf worden gestuurd, die met donderend geraas op een slee heen en weer werd bewogen over een rails, aangedreven door een vliegwiel dat 184 keer per minuut in de rondte draaide. De staaf bereikte zo drie keer per seconde een maximale snelheid van ruim 10 m/s. Precies op die momenten werd er een flitslicht (een puls van 0,01 seconde) door de staaf gestuurd.28 De optische inrichting was verder gelijk aan de proeven in water. De positie van de interferentiebanden hing af van de bewegingsrichting van de staaf ten opzichte van de lichtbron. Het robuuste apparaat was gemaakt door de firma Werkspoor – die wel van robuuste apparaten wist, en trouwens ook van rails. De experimenten waren niet zonder gevaar: de eerste de beste keer dat de opstelling op volle toeren draaide, knalde een glazen staaf los, verbrijzelde de andere delen, en sloeg de koperen eindstukken van het apparaat af. Er waren geen slachtoffers te betreuren, wel maanden van vergeefse labeur.29
Toestel ter bepaling van de lichtsnelheid in bewegende transparante media, vervaardigd door de Amsterdamse firma Werkspoor. (Museum Boerhaave V09749)
Wat was nu eigenlijk de reden om, na de succesvolle vaststelling van de dispersieterm in stromend water, alle inspanningen te getroosten om de proef in vaste stoffen te herhalen? Zeeman schrijft er het volgende over: ‘Vele gronden zijn er aan te voeren om een zoo uiterst moeilijke proef als die van Fizeau in de eerste plaats met water te verrichten; het is echter interessant ook de lichtbeweging in vaste, doorschijnende, snelbewegende stoffen te onderzoeken’.30 Punt. Met dit achteloze het-is-interessant moeten we het doen. Iedere verdere motivatie ontbreekt, en die zou ook moeilijk aan te geven zijn want diepere wetenschappelijk inzichten waren er niet mee gemoeid.
Met wat omrekenen en herformuleren als gevolg van het feit dat nu bewegende staven de verplaatsing van de interferentiebanden teweegbrachten in plaats van water, bleken de waarnemingen de theoretische waarden opnieuw dicht te naderen. Bij het experiment in glas, met λ = 4750 Å, en een (gereduceerde) snelheid van 1000 cm/s, leverde een reeks van 83 waarnemingen een faseverschuiving tussen de twee bundels op van 0,242 ± 0,004 (bij een iets andere berekeningswijze 0,243 ± 0,006). De theoretische bijdrage van de dispersieterm aan die faseverschuiving was 0,028, ofwel 11,5%. Zonder rekening te houden met de dispersieterm zouden de proeven ‘onverenigbaar’ zijn.31 Zeeman toonde zijn tevredenheid: ‘Het is niet te ontkennen dat, het bijzondere moeilijke van de proeven in aanmerking genomen, de overeenstemming tusschen theorie en waarneming zeer bevredigend is’.32 Wetenschappelijk relevant of niet, ook aan de vaste stoffen had Zeeman de dispersieterm ontfutseld.
Er ging voor Zeeman een verblindende werking uit van de technische-experimentele uitdagingen die de metingen hem stelden. Dit blijkt ook uit het contrast tussen de zorgvuldige wijze waarmee hij zijn apparaat bouwde en de gebrekkige wijze waarop hij zich het theoretische deel eigen maakte. Enkele maanden nadat Zeeman zijn resultaten openbaarde wees Max von Laue hem op een dissertatie uit 1912 van ene Franz Harress, een jonge astronoom die het leven had gelaten tijdens de Eerste Wereldoorlog. Harress had een vergelijkbaar experiment als Zeeman gedaan, maar dan met een snel roterende ring van prisma’s waar de stralen van een gesplitste lichtbundel in tegengestelde richtingen doorheen werden gestuurd. Zeeman kon er weinig aan doen, bezwoer Von Laue hem, dat hij Harress’ werk had gemist. Omdat de metingen Harress’ theoretisch afgeleide waarden tegenspraken, was publicatie van zijn werk achterwege gelaten.33
Twee weken later bracht echter ook Zeemans Groningse collega Frits Zernike (1888–1966) hem het werk van Harress onder de aandacht.34 Zernike was erop gestuit in de Astronomische Nachrichten van 1914, waarin Harress’ resultaten waren besproken door Paul Harzer (1857–1937). De teneur was dat Harress een theoretische fout had gemaakt, en dat na correctie hiervoor de resultaten prima klopten. Op Harzers bijdrage was een reactie van Einstein gevolgd die enkele (in zijn ogen) misverstanden in het artikel uit de weg ruimde en liet zien dat het resultaat zijn relativiteitstheorie ondersteunde.35 Een obscure Duitse dissertatie was nog te missen, maar deze stukken had Zeeman niet mogen ontgaan, ondanks de belemmeringen van het internationale wetenschappelijke verkeer als gevolg van de Eerste Wereldoorlog. Zernike voegde er aan toe dat Zeemans resultaten wel een veel grotere precisie gaven. En daarbij bleef het dan wat betreft de experimenten in vaste media.36
Net zoals bij de eerdere serie proeven stuurde Zeeman Einstein zijn resultaten. ‘Vielen Dank für die Zusendung Ihrer beiden Arbeiten über den Mitführungs-Koeffizienten bei festen Körpern’, luidde het antwoord een tikje afgemeten. Van een ‘unangenehm fühlbare Lücke’ repte Einstein nu niet – maar daar was ook geen reden voor.37
Dat de onweerstaanbare lokroep van technisch-experimentele uitdagingen Zeeman het grotere verband uit het oog liet verliezen stond niet op zichzelf. Een vergelijkbaar lot was een serie experimenten beschoren waarin hij de equivalentie van ‘trage’ en ‘zware’ massa aan toetsing onderwierp. Trage massa is de tegenwerking van materie tegen versnelling, zware massa de eigenschap dat materie andere materie aantrekt. De equivalentie van beide massa’s vormt een hoeksteen van de algemene relativiteitstheorie, het wachten was nog op experimenteel bewijs. Zeeman voerde experimenten die hierin moesten voorzien uit in 1917, tussen de twee series Fizeau-proeven door (in de hal van zijn buitenhuis in Huis ter Heide overigens – daar trilde de vloer tenminste niet).38 Zeeman onderzocht of er een discrepantie tussen beide soorten massa’s optrad als tijdens radioactieve processen trage massa wordt omgezet in energie. Zeemans opstelling bestond uit een torsiebalans – een kopie van de opstelling die de Hongaarse fysicus Loránd (of Roland) von Eötvös (1848–1919) gebruikte toen hij in 1890 de equivalentie van beide soorten massa’s had getest tot een precisie van 1: 2.107. Theoretisch laat zich afleiden dat massa’s aan de armen van de balans een torsiekracht ondervinden als er een verschil is in de verhouding tussen trage en zware massa (dit heeft te maken met de draaiing van de aarde). Zeeman vergeleek radioactieve uraniumverbindingen met niet-radioactieve loodverbindingen, en vond geen torsiekracht, met een (maximale) precisie van 1 : 5·106. Vervolgens herhaalde Zeeman de proef met anisotrope kristallen. Hij achtte het mogelijk dat de gravitatiekracht zich ongelijk in de verschillende richtingen door anisotrope stoffen uitspreidde. Volgens Anne Kox toont deze laatste gedachtegang bovenal aan dat Zeeman de algemene relativiteitstheorie niet goed beheerste. Bovendien was het hem ontgaan dat Von Eötvös en zijn medewerkers al een decennium eerder proeven met radioactieve stoffen hadden gedaan (verzachtende omstandigheid was dat deze tot 1922 alleen in samenvatting waren gepubliceerd). Zeemans precisie was niet eens significant beter.39
Zeeman-Telescope?
Drie jaar na Einsteins bezoek aan het in alle voegen krakende Natuurkundig Laboratorium opende Zeemans nieuwe onderzoekslaboratorium ‘Physica’ zijn deuren. Steeds meer beperkte zijn blik zich tot de – toegegeven ongeëvenaarde – onderzoekscapaciteiten die zijn nieuwe instituut hem bood om zijn kunsten te tonen.40 Steeds minder richtte hij zich op de opwindende nieuwe ontwikkelingen in de natuurkunde. Almaar meer esoterische proeven aan het Zeemaneffect en analyses van complexe spectra voerden de boventoon. In hetzelfde jaar 1923 publiceerde Einstein zijn eerste originele artikel over de unificatietheorie waarin hij zich de rest van zijn leven zou vastbijten. Ten tijde van Einsteins bezoek aan Zeeman stonden beide heren dus op het punt om zich enigszins te isoleren van de actuele ontwikkelingen en zich in hun eigen wereld op te sluiten.
De succesvolle detectie van gravitatiegolven door LIGO betekende een forse steun in de rug voor de plannen voor een Europese opvolger, waarover al enige jaren wordt nagedacht. Mogelijk zal de ‘Einstein-telescope’, zoals het nieuwe observatorium voor gravitatiegolven moet gaan heten, in Nederland worden geplaatst – onder de Vaalserberg. Mocht het zover komen dan willen we een andere naam voorstellen: inderdaad, ‘Zeeman-Telescope’, naar de Nederlandse pionier van het experimentele relativistische onderzoek. Als eerbetoon, maar ook als waarschuwing.41
Bijlage: De bepaling van de lichtsnelheid in stromend water
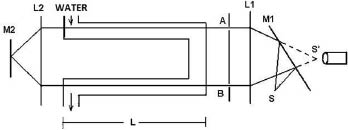
Zeemans baseerde zowel zijn opstelling als zijn meetmethode voor de metingen van de lichtsnelheid in water op een gelijkaardig experiment van Michelson en Morley uit 1886, die op hun beurt voortborduurden op eerdere experimenten van Fizeau.42 Kern van de opstelling zijn twee identieke (horizontale) buisdelen waardoor in tegengestelde richting water stroomt. Figuur 5 geeft de schematische opstelling. In M1 wordt een door S uitgezonden lichtbundel gesplitst. Het deel van deze bundel dat spleet A passeert doorloopt hetzelfde traject als het deel dat door spleet B gaat, alleen gaat A tegen de waterstroom in, en B met de waterstroom mee. De lichtstralen komen via lens L2 in spiegel M2 (in het brandpuntsvlak van L2) terecht en na reflectie belanden ze in het andere buisdeel. Lens L1 recombineert de bundels in S', en versterkt de intensiteit van de interferentiebanden. Met een oculairlens kan de eventuele verschuiving van inferentiestrepen worden gemeten ten opzichte van de situatie waarin het water in rust is.
Vereenvoudigd schema van Zeemans variant op de opstelling van Michelson en Morley. Voor toelichting, zie de bijlage.
Met het water in rust ziet een waarnemer het typische interferentiepatroon van het klassieke geval waarin een lichtbundel in fase door twee spleten valt (fig. 6). Op het moment dat een van de golffronten vertraagd is ten opzichte van de ander, gaat dit patroon verschuiven. Mocht de ether worden meegesleept, dan zou het deel van het licht dat het traject met de waterstroom mee aflegt (en dus ook met de etherstroom meebeweegt) er korter over doen om S' te bereiken dan het deel dat tegen de stroom in gaat. Wanneer de ether gedeeltelijk zou worden meegesleept, dan was het effect minder groot dan bij volledige meesleping. Als de ether geheel niet werd meegesleept, dan zou er geen enkele verschuiving optreden in het interferentiepatroon. Belangrijk was dat bij dit experiment ook de verschuiving van de interferentiebanden volgens Fresnels formule voor gedeeltelijke meesleping kon worden berekend.
Interferentiepatroon gegenereerd door twee spleten. De richting van de verplaatsing (naar links of rechts) van de banden hangt af van de stroomrichting van het water.